はじめに
この記事は下記記事の補足説明です。
まずは↓こちらを読んで分からなかったら、本記事を読んでみてください。
気柱の重さが一番軽い\( P_\text{C} \)が、気圧が1000mで一番高いというところが、理解できません。
気圧は空気の重さと考えていますが、混乱します。
「気圧は空気の重さと考えています」
↑この考え方で合っています!この考え方をもとに問題を解いていきます。
問題文には「各地点の地上気圧が等しい」とあります。
気圧は空気の重さですので、この問題では地上〜はるか上空(高度数十km)までの空気の重さは同じという条件のもとで考えます。
つまり、地上〜はるか上空(高度1000mよりはるか上空)までにある空気の数(=重さ)は同じということです。
では、高度1000mでの気圧とは何でしょうか?
これは、高度1000mより上にある空気の重さということです。
地上気圧との違いは、地上〜高度1000mまでの空気の重さを考えてるかどうかの違いです。
地上気圧は高度0m〜はるか上空までの空気の重さであり、
高度1000mでの気圧は高度1000m〜はるか上空までの空気の重さということです。
 てるらん
てるらんじゃあ、地点A、B、Cの地上気圧は等しいのに、どうして高度1000mの気圧は異なるの?



それは、地点A、B、Cの地上〜高度1000mまでの気層の気温と混合比が違うからだよ!
では、具体的に問題を解いてみましょう。
\( P_\text{A} \) と \( P_\text{B} \) の大小関係について
(問題)地点 \( \text{A}\)、\( \text{B}\) における地上(高度0m)から高度1000mまでの気層の気温の平均値がそれぞれ \( T_\text{A}\)、\( T_\text{B}\)、混合比がそれぞれ \(q_\text{A}\)、\( q_\text{B}\) であり、また、\( T_\text{A}<T_\text{B} \) かつ \( q_\text{A}=q_\text{B} \) となっている。各地点の地上気圧が等しいとき、地点 \( \text{A} \)、\( \text{B} \) における高度1000mの気圧 \( P_\text{A} \)、\( P_\text{B} \) の大小関係を求めよ。
地点Aと地点Bの地上〜高度1000mまでの気層では、混合比が同じで、気温が異なります。
ですので、\( P_\text{A} \) と \( P_\text{B} \)では、気温差による気圧の違い を考えます。


ここからは、上図(=図1)を見ながら考えてみてください。
地点Aと地点Bの地上〜高度1000mまでの気層には気温差があります。
空気は、気温が高くなると膨張し、気温が低くなると圧縮します。
空気が膨張するということは単位体積あたりの分子(=乾燥空気や水蒸気の粒)の数は少なくなります。
逆に、空気が圧縮すると、単位体積あたりの分子(=乾燥空気や水蒸気の粒)の数は多くなります。
気温差は \( T_\text{A} < T_\text{B} \) ですので、地点Bの方が地上〜高度1000mまでの空気が膨張しています。
言い換えると、地点Bの方が地上〜高度1000mまでの分子の個数が少ないということです。
しかし、混合比は同じ(\( q_\text{A} = q_\text{B} \))なので、地点Aと地点Bの地上〜高度1000mまでの乾燥空気と水蒸気の存在比は同じになります。
このことから、地点Aと地点Bの地上〜高度1000mまでの分子の分布を描くと上図(=図1)のように描くことができます。
気温差は \( T_\text{A} < T_\text{B} \) なので、地点Bの方が分子数は少ないです。
混合比は同じ(\( q_\text{A} = q_\text{B} \))なので、地上〜高度1000mまでの乾燥空気と水蒸気の存在比が同じです。
例えば、上図を見てみると、地点Aは乾燥空気の粒が6個、水蒸気の粒が4個あります。
これをもとに地点Aの混合比を計算してみると、地点Aの混合比は \( \frac{4}{6} = \frac{2}{3} \) となります。
一方、地点Bは乾燥空気の粒が3個、水蒸気の粒が2個あります。
これをもとに地点Bの混合比を計算してみると、地点Bの混合比は \( \frac{2}{3} \) となり、地点Aの混合比と一致します。
ここからが大事!!!
地上気圧は同じなので、仮に地上〜はるか上空(高度数十km)までの分子の個数を20個として考えてみましょう。
このとき、乾燥空気と水蒸気はそれぞれ10個ずつあるとします。
また、乾燥空気は水蒸気より重いので、乾燥空気の重さを2、水蒸気の重さを1として考えます。
図1を見てみると、地点Aは地上〜高度1000mまでの間に乾燥空気が6個、水蒸気が4個あります。
つまり、高度1000m〜はるか上空までの間には乾燥空気が10-6=4個、水蒸気が10-4=6個あるということです。
したがって、地点Aの高度1000mでの気圧\( P_\text{A} \) は、高度1000m〜はるか上空までの空気の重さですので、4×2+6×1=14 となります。(×2や×1は乾燥空気と水蒸気の重さを掛けています。)
同様に、地点Bは地上〜高度1000mまでの間に乾燥空気が3個、水蒸気が2個あります。
つまり、高度1000m〜はるか上空までの間には乾燥空気が10-3=7個、水蒸気が10-2=8個あるということです。
したがって、地点Bの高度1000mでの気圧\( P_\text{B} \) は、7×2+8×1=22 となります。
以上より、高度1000m〜はるか上空までの空気が重たいのは地点Bなので、\( P_\text{A} \) < \( P_\text{B} \) となります
\( P_\text{B} \) と \( P_\text{C} \) の大小関係について
(問題)地点 \( \text{B}\)、\( \text{C}\) における地上(高度0m)から高度1000mまでの気層の気温の平均値がそれぞれ \( T_\text{B}\)、\( T_\text{C}\)、混合比がそれぞれ \(q_\text{B}\)、\( q_\text{C}\) であり、また、\( T_\text{B}=T_\text{C} \) かつ \( q_\text{B}<q_\text{C} \) となっている。各地点の地上気圧が等しいとき、地点 \( \text{B} \)、\( \text{C} \) における高度1000mの気圧 \( P_\text{B} \)、\( P_\text{C} \) の大小関係を求めよ。
地点Bと地点Cの地上〜高度1000mまでの気層では、気温が同じで、混合比が異なります。
ですので、\( P_\text{B} \) と \( P_\text{C} \)では、混合比差による気圧の違い を考えます。
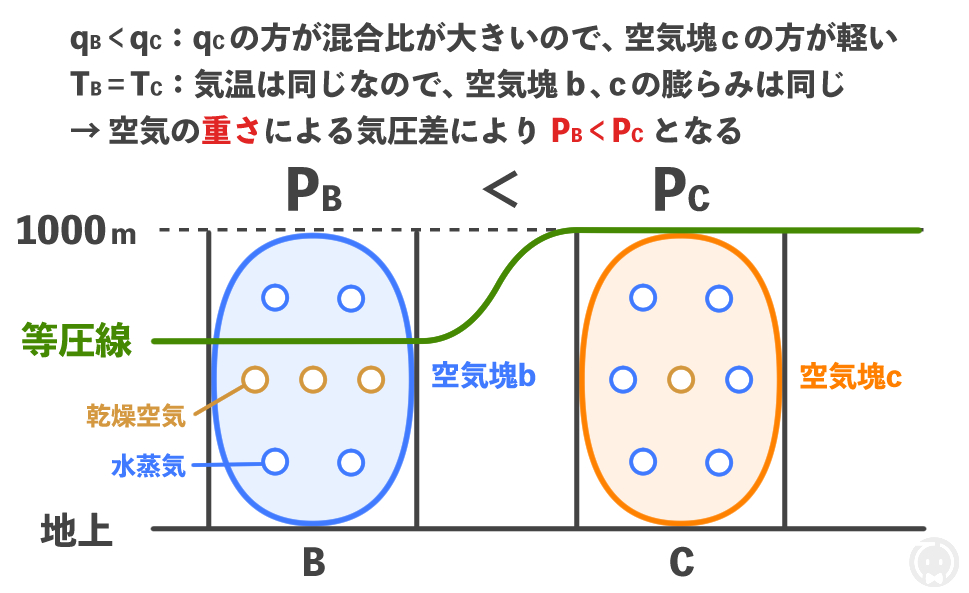

ここからは、上図(=図2)を見ながら考えてみてください。
地点Bと地点Cの地上〜高度1000mまでの気層は気温が同じです。
つまり、地点Bと地点Cの地上〜高度1000mまでの分子の個数は同じです。
しかし、混合比が\( q_\text{B} < q_\text{C} \)なので、地点Cのほうが水蒸気を多く含んでいます。
このことから、地点Bと地点Cの地上〜高度1000mまでの分子の分布を描くと上図(=図2)のように描くことができます。
気温は同じ \( T_\text{B} = T_\text{C} \) なので、地点Bと地点Cの分子数は同じです。
混合比は\( q_\text{B} < q_\text{C} \)なので、地点Cのほうが水蒸気が多いです。
ここからが大事!!!
地上気圧は同じなので、仮に地上〜はるか上空(高度数十km)までの分子の個数を20個として考えてみましょう。
このとき、乾燥空気と水蒸気はそれぞれ10個ずつあるとします。
また、乾燥空気は水蒸気より重いので、乾燥空気の重さを2、水蒸気の重さを1として考えます。
図2を見てみると、地点Bは地上〜高度1000mまでの間に乾燥空気が3個、水蒸気が4個あります。
つまり、高度1000m〜はるか上空までの間には乾燥空気が10-3=7個、水蒸気が10-4=6個あるということです。
したがって、地点Bの高度1000mでの気圧\( P_\text{B} \) は、高度1000m〜はるか上空までの空気の重さですので、7×2+6×1=20 となります。(先ほど求めた地点Bの気圧\( P_\text{B} \)=22と異なるのは、あくまで地点Aや地点Cとの気圧の大小を比較するための計算だからです。)
同様に、地点Cは地上〜高度1000mまでの間に乾燥空気が1個、水蒸気が6個あります。
つまり、高度1000m〜はるか上空までの間には乾燥空気が10-1=9個、水蒸気が10-6=4個あるということです。
したがって、地点Cの高度1000mでの気圧\( P_\text{C} \) は、9×2+4×1=22 となります。
以上より、高度1000m〜はるか上空までの空気が重たいのは地点Cなので、\( P_\text{B} \) < \( P_\text{C} \) となります。
これらより、\( P_\text{A} < P_\text{B} \) かつ \( P_\text{B} < P_\text{C} \) であるため、答えは \( P_\text{A} < P_\text{B} < P_\text{C} \) となります。




コメント