問5
地球と同じ大きさで放射平衡温度も等しい惑星が、太陽から地球までの距離の半分の距離に位置しているとする。地球のアルベドを 0.30 としたとき、この惑星のアルベドとして適切なものを、下記の1〜5の中から1つ選べ。なお、地球及びこの惑星は球形の黒体とする。
アルベド(予備知識)
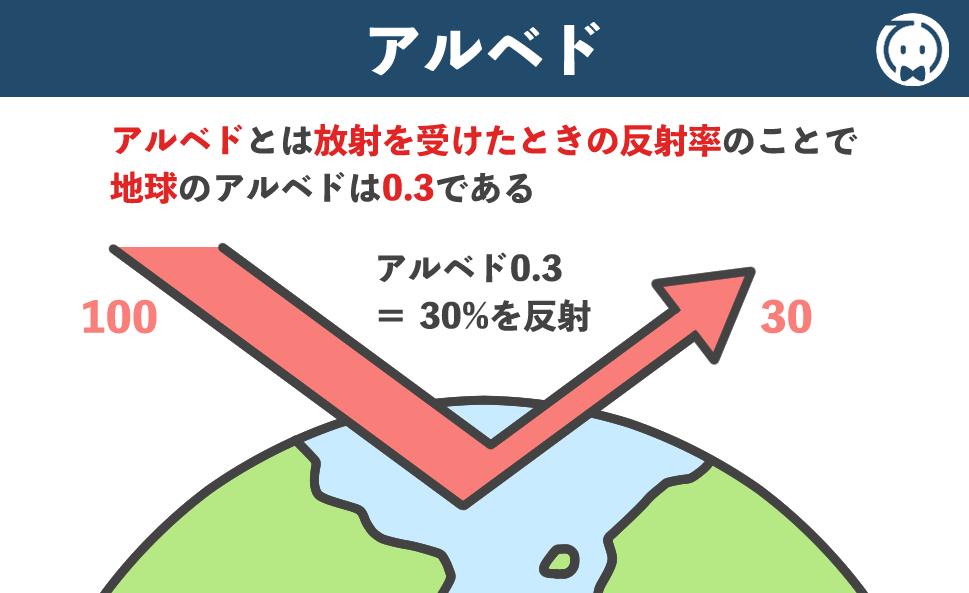
アルベドとは、放射を受けたときの反射率のことです。
アルベドが1であれば、すべての放射を反射し、アルベドが0であれば、すべての放射を吸収することを意味します。
地球のアルベドは0.3です。
つまり、地球は宇宙から受けた放射のうち、その30%が吸収されずに宇宙に反射されるということです。
下表はさまざまな場所や状況によるアルベドの一覧です。
| 場所・状況 | アルベド |
|---|---|
| 裸地※ | 0.1〜0.25 |
| 砂、砂漠 | 0.25〜0.4 |
| 森林地 | 0.1〜0.2 |
| 新雪 | 0.8〜0.95 |
| 海面(高度角25°以上) | 0.1以下 |
| 海面(高度角25°以下) | 0.1〜0.7 |
| 厚い雲 | 0.8前後 |
| 地球平均 | 0.3 |
| 金星平均 | 0.78 |
| 火星平均 | 0.16 |
ステファン・ボルツマンの法則(予備知識)
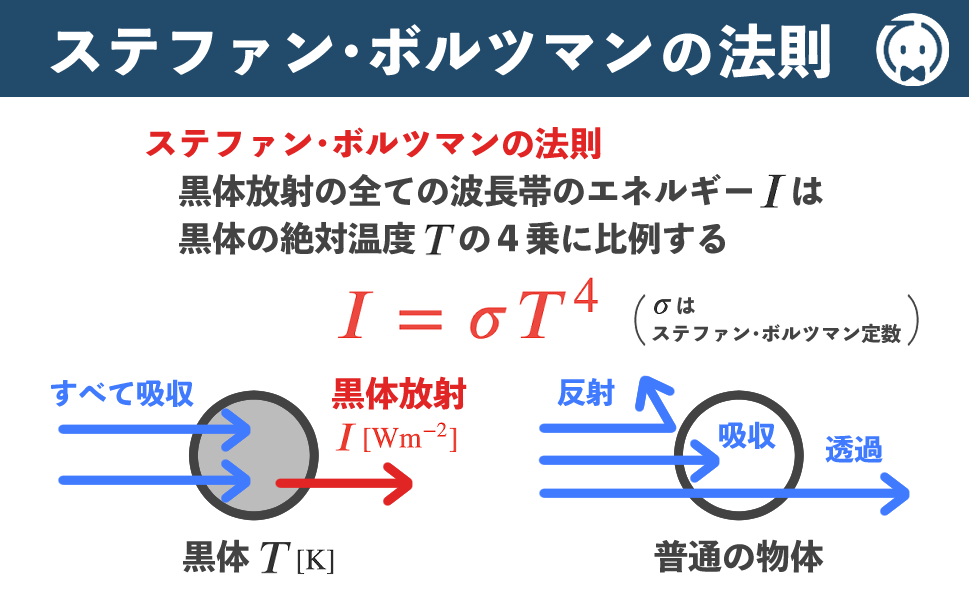
すべての物体は、その温度に応じた電磁波を放射しています。
同時に物体は入射してきた電磁波を吸収する性質も持ちます。
この入射してくる放射エネルギーをすべて余すことなく吸収する仮想的な物体を黒体(読:こくたい)といいます。
黒体は与えられた温度に応じた最大の放射エネルギーを放出します。
この放射のことを黒体放射(読:こくたいほうしゃ)といいます。
黒体放射の全ての波長帯のエネルギーの総量は、黒体の絶対温度の4乗に比例します。
これをステファン・ボルツマンの法則といいます。
(1879年にステファンが実験的に、1884年にボルツマンが理論的にこの法則を導いたためにステファン・ボルツマンの法則とよばれています。)
ある黒体の単位面積が単位時間に放射するエネルギー(=地球から放出される長波放射エネルギー)を I [ Wm-2 ] 、黒体の絶対温度(=放射平衡温度)を T [ K ]、ステファン・ボルツマン定数を
σ = 5.67×10-8 [ Wm-2 K-4 ] とすると、次の関係が成り立ちます。
I = σT4
放射平衡(予備知識)
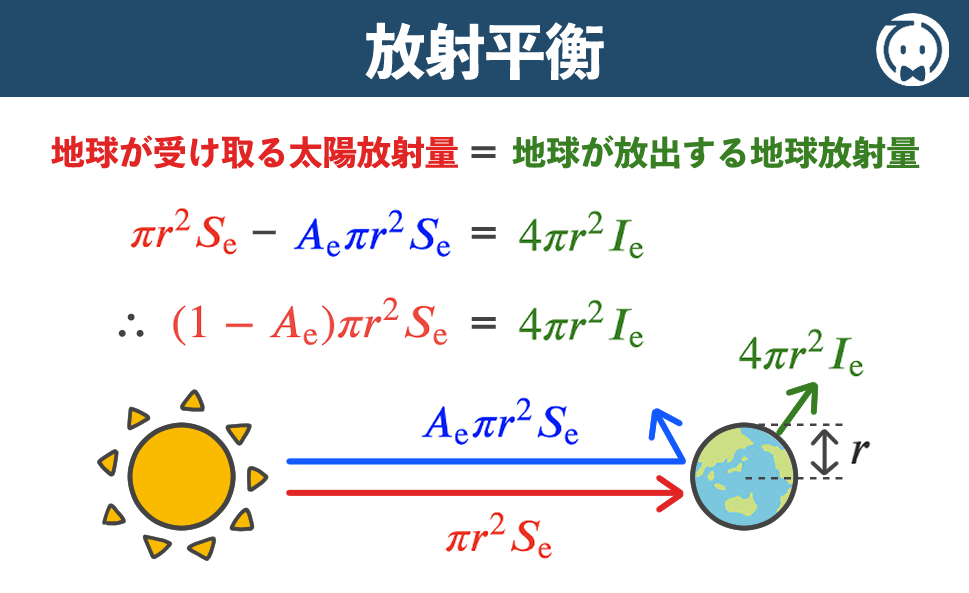
大気の存在しない真空の地球表面では、1秒あたりに地球が受け取る太陽放射量と、放出する地球放射量が釣り合い、放射平衡(読:ほうしゃへいこう)が成り立つと考えられ、次の関係が成り立ちます。
\( (1 – A_\text{e}) \pi r^{\,2} S_\text{e} = 4 \pi r^{\,2} I_\text{e} \)
ここで、\( A \) は地球のアルベド、\( r \) は地球の半径、\( S_\text{e} \) は地球 \( \text{e} \) の位置での1m2 あたりに受ける太陽放射強度 [W m-2] 、\( I_\text{e} \) [W m-2] を地球の放射強度とします。
左辺は地球が受け取る太陽放射量、右辺は地球が放射する放出する地球放射量を表しています。
ここで具体的な値を入れて、計算してみましょう。
まずは、両辺の \( \pi r^{\,2} \) を消去し、両辺を入れ替えて整理すると
\( I_\text{e} = \displaystyle \frac{S_\text{e}(1-A)}{4} \)
となります。
これに \( A \) = 0.30 、\( S_\text{e} \) = 1.38 × 103 [W m-2] を代入すると
\begin{align} I_\text{e} &= \displaystyle \frac{1.38×10^{\;\,3} × (1 – 0.30)}{4} \\ &= 241.5\, [\, \text{W m}^{\;\,-2} \,] \end{align}
となります。
これは、地球放射強度を示し、地球の表面から、1m2 あたり 241.5 W に相当する熱が宇宙に逃げていることを表します。
放射強度は距離の2乗に反比例して減少する(予備知識)
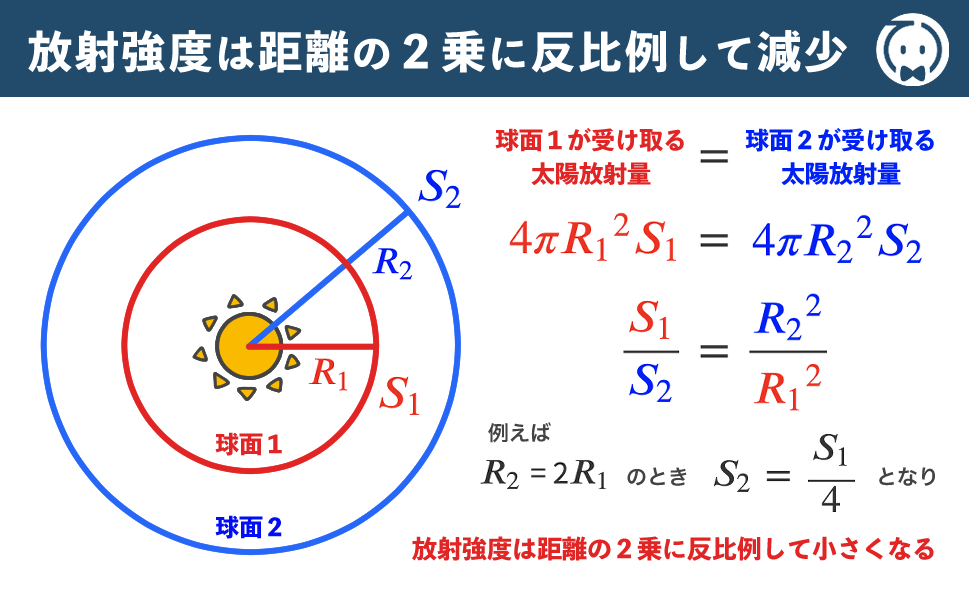
太陽を中心にして半径がそれぞれ \( R_1 \)、\( R_2 \) の球面 \( 1 \)、\( 2 \) を考え、
球面 \( 1 \)、\( 2 \) 上の放射強度(=単位面積・単位時間当たりに入射する放射エネルギー量)を \( S_1 \)、\( S_2 \) とします。
太陽と球面までの空間における散乱や吸収を無視すれば、球面 \( 1 \)、\( 2 \) が受ける放射エネルギーは太陽からの放射エネルギーに等しいので
\( 4 \pi {R_1}^2 S_1 = 4 \pi {R_2}^2 S_2 \)
( \( S_1 ,\, S_2\):太陽からそれぞれ距離 \( R_1,\, R_2 \) 離れた、太陽を中心とする球面に単位時間・単位面積当たりに入射する放射エネルギー量 [ J m-2 s-1 ] )
となり、式変形すると
\( \displaystyle \frac{S_1}{S_2} = \frac{{R_2}^2}{{R_1}^2} \)
となります。
例えば、\( R_2 \) = 2\( R_1 \)とすると、
\( \displaystyle S_2 = \frac{S_1}{4} \)
となります。
したがって、放射強度は距離の2乗(=22)に反比例して、距離とともに減少します。
本問の解説
(問題)地球と同じ大きさで放射平衡温度も等しい惑星が、太陽から地球までの距離の半分の距離に位置しているとする。地球のアルベドを 0.30 としたとき、この惑星のアルベドを求めよ。なお、地球及びこの惑星は球形の黒体とする。
→ 答えは 0.83 です。
地球 \( \text{e} \) の位置での1m2 あたりに受ける太陽放射強度を \( S_\text{e} \) [ W m-2 ] 、地球の半径を \( r \)(したがって、断面積は \( \pi r^{\,2} \))、地球のアルベドを \( A_\text{e} \) とすると、地球に入射する太陽放射量は \( \pi r^{\,2} S_\text{e} \) となります。
このうち、\( A_\text{e} \pi r^{\,2} S_\text{e} \) は地球に吸収されずに宇宙空間に反射されるので、地球が吸収する太陽放射量は \( \pi r^{\,2} S_\text{e} \,-\, A_\text{e} \pi r^{\,2} S_\text{e} \) つまり \( (1 – A_\text{e}\,) \pi r^{\,2} S_\text{e} \) となります。
また、地球の放射強度を \( I_\text{e} \) [ W m-2 ] とすれば、地球の表面積は \( 4 \pi r^{\,2} \) なので、地球が放出する放射量は \( 4 \pi r^{\,2} I_\text{e} \)となります。
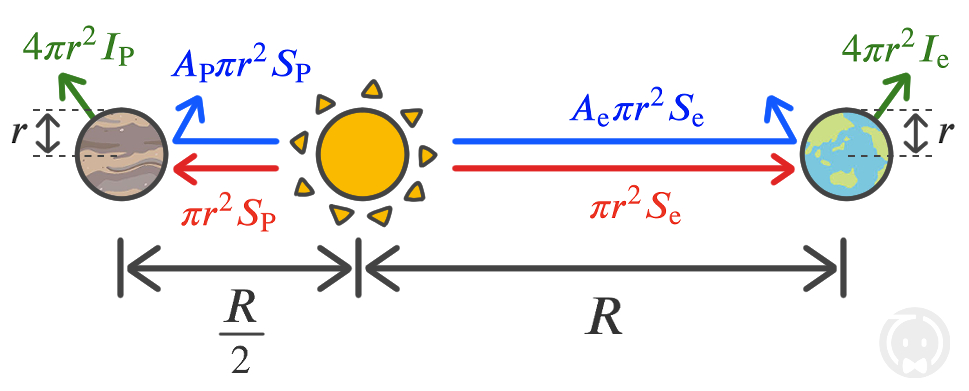
放射平衡では、地球が吸収する太陽放射量と、放出する地球放射量が釣り合っているので、下記式が成り立ちます。
\( (1 – A_\text{e}) \pi r^2 S_\text{e} = 4 \pi r^2 I_\text{e} \tag{1} \)
同様に、惑星 \( \text{P} \) の位置での太陽放射強度を \( S_\text{P} \)、惑星 \( \text{P} \) のアルベドを \( A_\text{P} \)、惑星 \( \text{P} \) の放射強度を \( I_\text{P} \) とすれば、惑星 \( \text{P} \) の半径も地球と同じ \( r \) なので、下記式が成り立ちます。
\( (1 – A_\text{P}) \pi r^2 S_\text{P} = 4 \pi r^2 I_\text{P} \tag{2} \)
ここで、太陽と地球および惑星 \( \text{P} \) との間の空間で、太陽放射が散乱や吸収を受けないと仮定すれば、太陽を中心に地球までの距離 \( R \) を半径とする球面と、太陽を中心に惑星 \( \text{P} \) までの距離 \( \frac{R}{2} \) を半径とする球面に到達する太陽放射量は等しいので、
\( 4 \pi R^2 S_\text{e} = 4 \pi \displaystyle \bigg( \frac{R}{2} \bigg)^2 S_\text{P} \)
となり、これを整理すると、下記式となります。
\( S_\text{e} = \displaystyle \frac{S_\text{P}}{4} \tag{3} \)
また、黒体放射強度に関するステファン・ボルツマンの法則によれば、黒体放射強度 \( I \) [ W m-2 ] は、その黒体の絶対温度 \( T \) [ K ] の4乗に比例しており、\( \sigma \) をステファン・ボルツマン定数とすると、 \( I = \sigma T^4 \) が成り立ちます。
以上より、黒体の温度 \( T \) が等しければ、黒体放射強度 \( I \) も等しいことが分かります。
本問では、地球 \( \text{e} \) と惑星 \( \text{P} \) はともに黒体で、その放射平衡温度も等しいので、両者からの放射強度(黒体放射強度) \( I_\text{e} \) と \( I_\text{P} \) も等しくなります。
\( I_\text{e} = I_\text{P} \tag{4} \)
(1)、(2)の辺々をそれぞれ割って、(3)、(4)を代入し、整理すると
\(1 – A_\text{e} = 4(1 – A_\text{P}) \tag{5} \)
となる。地球 \( \text{e} \) のアルベドは 0.30 なので、\( A_\text{e} \) = 0.30 を(5)に代入すると、
\begin{align} 1 – 0.30 &= 4(1 – A_\text{P}) \\ A_\text{P} &= 0.825 \end{align}
となります。
したがって、惑星 \( \text{P} \) のアルベドは 0.83 なので、答えは 4 となります。
書いてある場所:P105(放射強度は距離の2乗に反比例して、距離とともに減少)、P110(黒体、黒体放射)、P113〜114(アルベド、放射平衡)
書いてある場所:P90〜92(ステファン・ボルツマンの法則、放射平衡、アルベド)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。





コメント