問2
大気中の水蒸気量の指標のひとつである湿球温度について述べた次の文章の下線部(a)〜(c)の正誤の組み合わせとして正しいものを、下記の1〜5の中から1つ選べ。
湿球温度計に通風される未飽和の空気(温度 \( T_0\) )の混合比を \( W_1\) 、湿球を通過した空気の混合比を \( W_2\) とし、 \( W_1\) 、\( W_2\) それぞれを飽和混合比とする温度を \( T_1\) 、\( T_2\) とすると、 (a) \(T_1\) は仮温度、\(T_2\) は湿球温度 で、 (b) \(T_1 < T_2\) である。混合比の差 \( \Delta W = W_2 – W_1\) に相当する水の蒸発によって温度が変化していることから、蒸発の潜熱を \(L\) 、定圧比熟を\(C_p\) とすれば、 (c) \(L \Delta W = C_p ( T_0 – T_2 ) \) という関係が成り立つ。
混合比(予備知識)
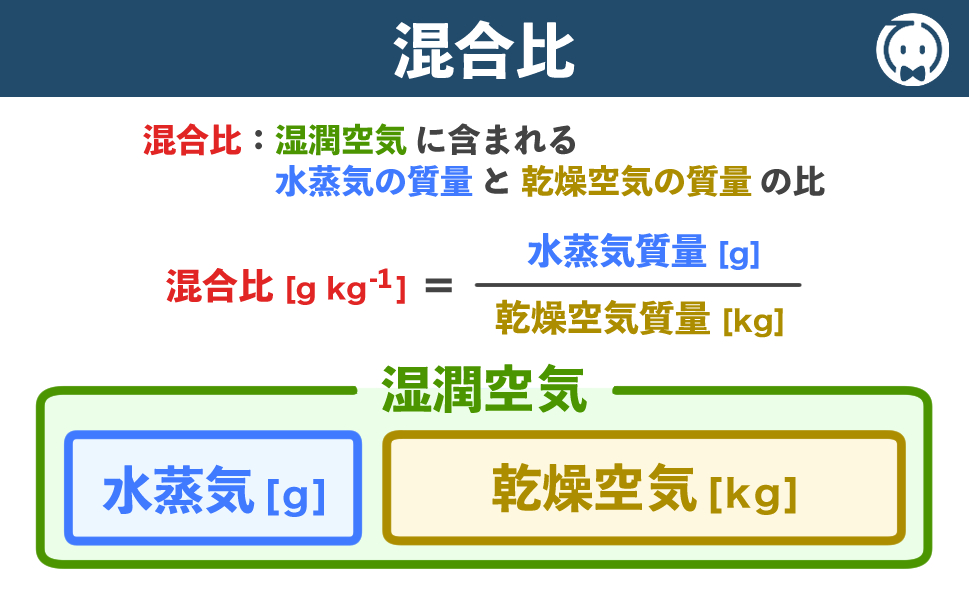
混合比(読:こんごうひ)とは湿潤空気に含まれる「水蒸気の質量」と「乾燥空気の質量」の比のことです。
 てるるん
てるるん簡単に言うと、水蒸気を含んでいる湿った空気の中で、乾燥空気と水蒸気が何:何の割合で存在しているかを表したものだよ!
式で書くとこうなります。
\(\text{混合比}=\displaystyle\frac{\text{水蒸気質量 [g]}}{\text{乾燥空気質量 [㎏]}}\)
飽和混合比(予備知識)
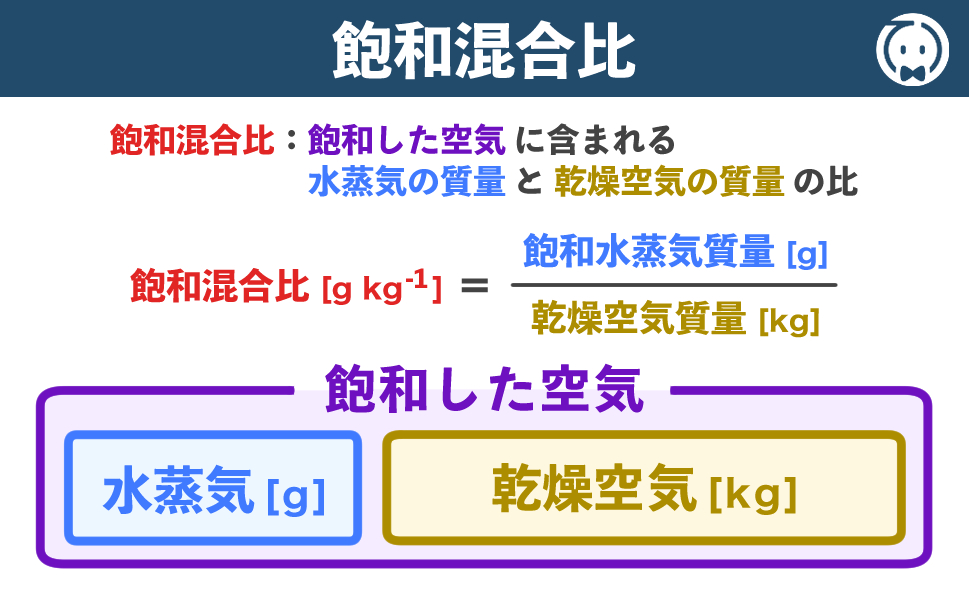

飽和混合比(読:ほうわこんごうひ)とは飽和した湿潤空気に含まれる「水蒸気の質量」と「乾燥空気の質量」の比のことです。



簡単に言うと、飽和した空気の中で、乾燥空気と水蒸気が何:何の割合で存在しているかを表したものだよ!
(飽和とは、相対湿度が100%で、水面から大気中への蒸発が行われない状態のことです。)
飽和混合比を式で書くとこうなります。
\(\text{飽和混合比}=\displaystyle\frac{\text{飽和水蒸気質量 [g]}}{\text{乾燥空気質量 [㎏]}}\)
露点温度(予備知識)
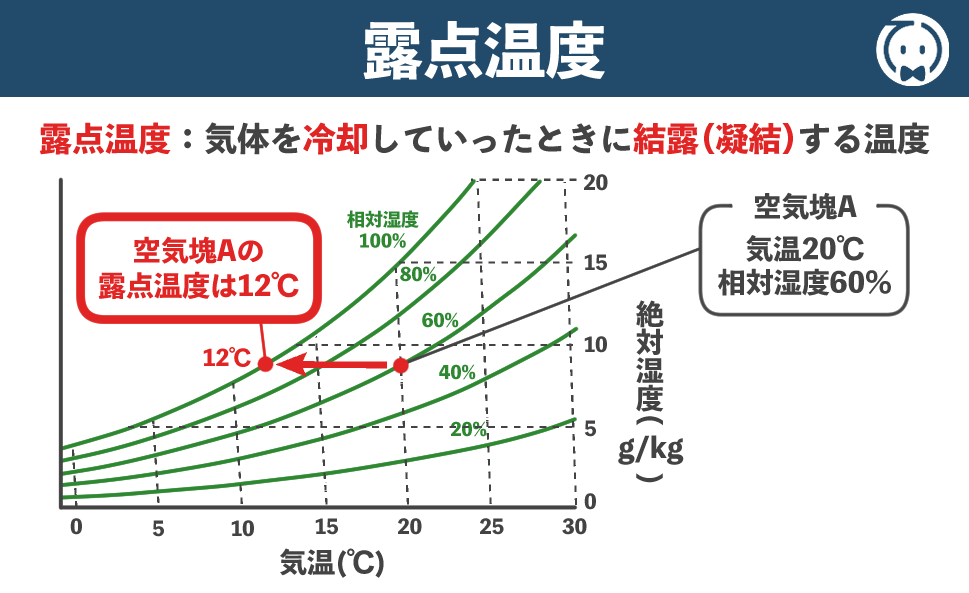

露点温度(読:ろてんおんど)とは気体を冷却していったときに結露(凝結)する温度のことです。
結露(凝結)するということは、相対湿度は100%です。



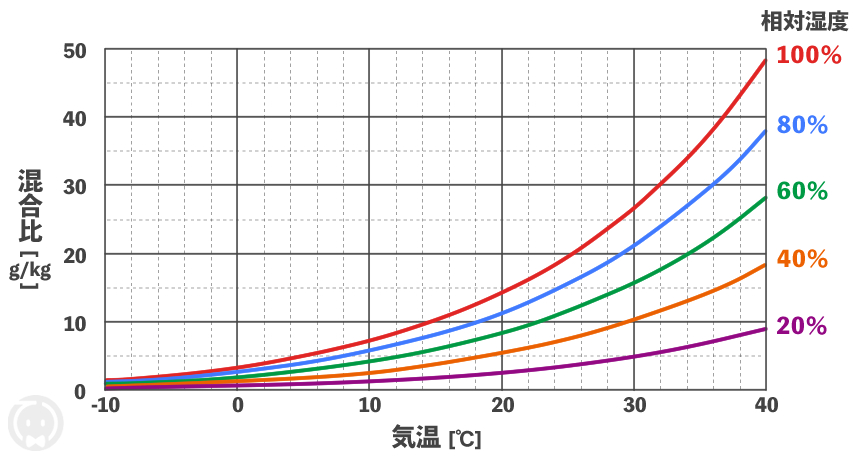
例えば、空気塊A(気温20℃、相対湿度60%)の露点温度を上図のグラフで考えてみよう!
温度20℃の線と相対湿度60%の曲線が交わった点から、左側にまっすぐラインを引き、相対湿度100%の線と交わった点が露点温度(結露が発生する温度)となります。
仮温度(予備知識)
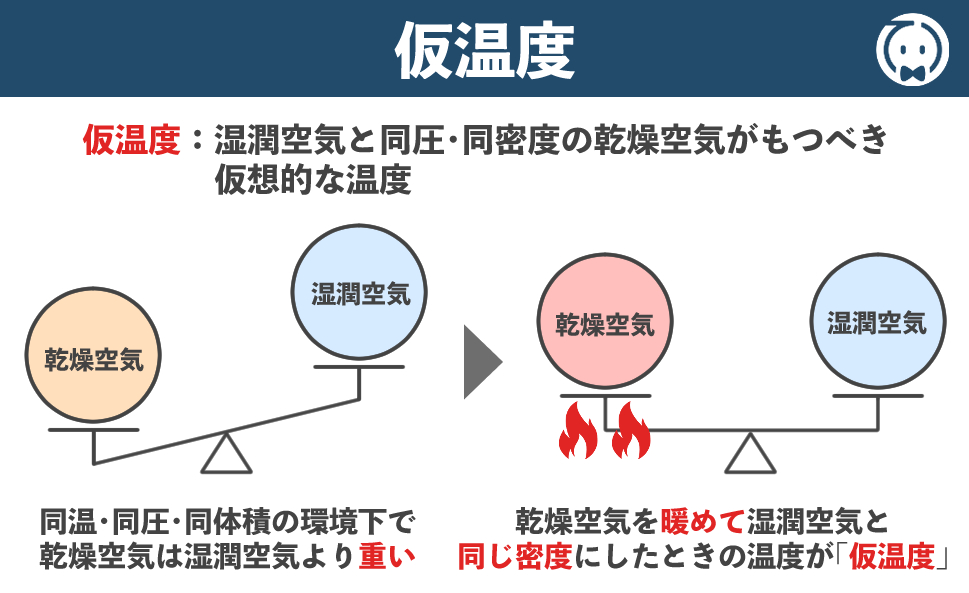

仮温度(読:かりおんど)とは湿潤空気と同圧・同密度の乾燥空気がもつべき仮想的な温度のことです。
同温・同圧・同体積の環境下では、乾燥空気は湿潤空気より重いです。
また、乾燥空気と湿潤空気では気体定数の値が異なります。
そこで、乾燥空気を暖めて膨張させ、密度を湿潤空気と同じにすることで、計算を簡単にするのです。
この、暖めて膨張させた乾燥空気の温度を仮温度といいます。
湿球温度(予備知識)
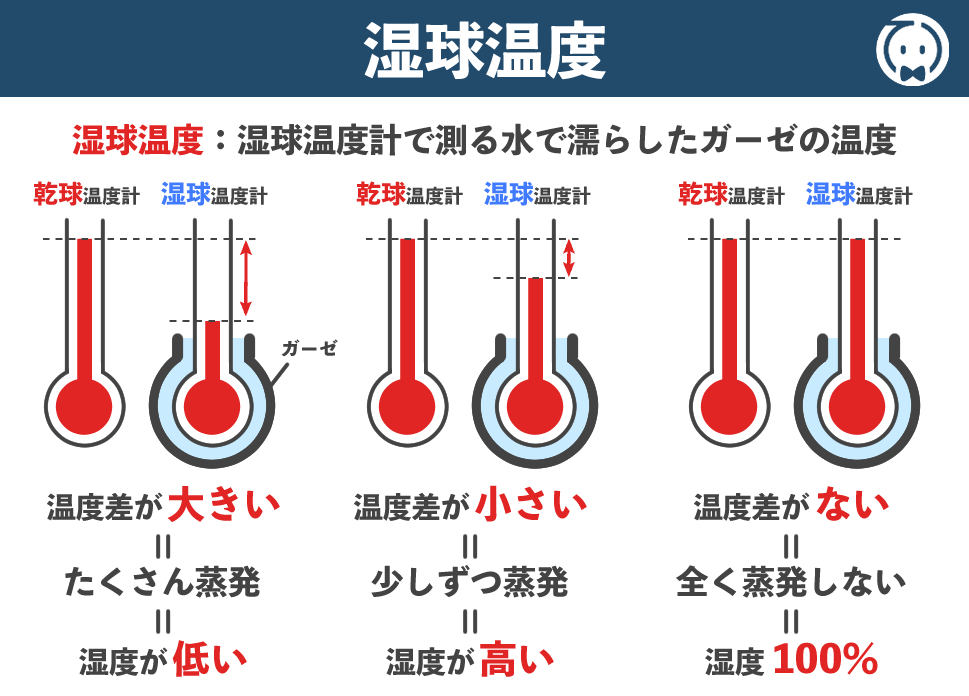

湿球温度(読:しつきゅうおんど)とは水で濡らしたガーゼの温度のことです。
濡れたガーゼの水が蒸発するときに熱を奪うので、湿球温度計の温度は、乾球温度計の温度(=気温)より低くなります。
また、空気が乾燥しているほど、水分が蒸発して熱が多く奪われるので、湿球温度計の温度は低くなります。
したがって,乾球温度計と湿球温度計の温度差が大きいほど湿度は低く、温度差が小さいほど湿度は高くなります。
本問の解説:(a) について
(a) 湿球温度計に通風される未飽和の空気(温度 \( T_0\) )の混合比を \( W_1\) 、湿球を通過した空気の混合比を \( W_2\) とし、 \( W_1\) 、\( W_2\) それぞれを飽和混合比とする温度を \( T_1\) 、\( T_2\) とすると、 (a) \(T_1\) は仮温度、\(T_2\) は湿球温度 である。
→ (a)は 誤 です。
問題文がややこしいので下図のグラフを使って説明してみます。

まずは、\( T_1\) から考えてみましょう。
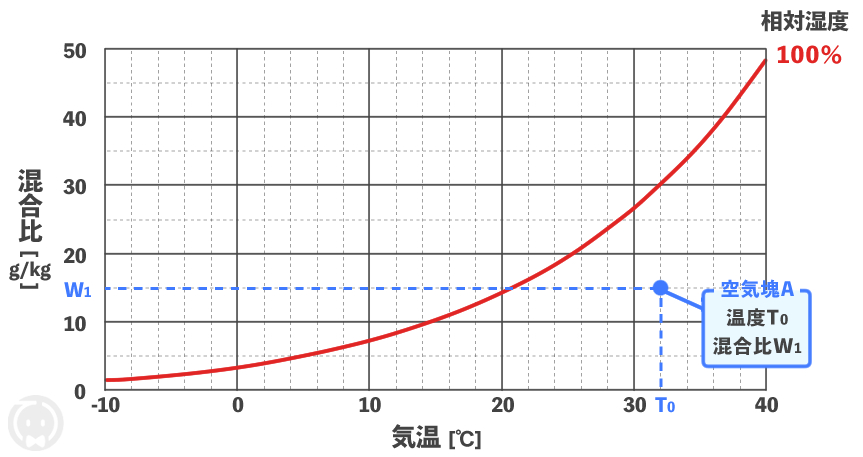
問題文は、湿球温度計に吹いてくる未飽和の空気の混合比を \( W_1\) とするとき、混合比 \( W_1\) が飽和混合比となる温度 \( T_1\) を何と言いいますか?という意味です。
湿球温度計に吹いてくる空気塊 \( \text{A} \) (温度 \( T_0 \)、混合比 \( W_1 \))をプロットすると下図のようになります。

次に、混合比 \( W_1\) が飽和混合比となる温度 \( T_1\) は、このままグラフを左にずらしていき(=温度を低くしていき)、相対湿度100%の線とぶつかったときの温度です。
これをプロットすると下図のようになります。
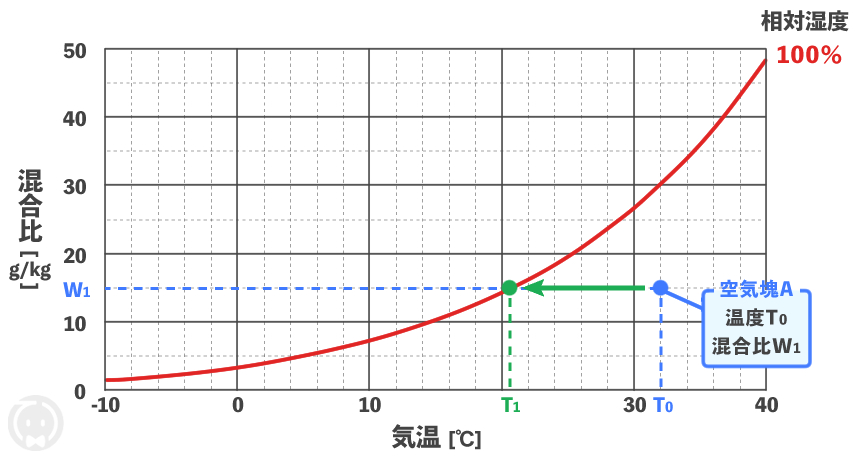

この温度 \( T_1\) は、空気が冷却され水蒸気が結露(凝結)するときの温度ですので、 \( T_1\) は空気塊 \( \text{A} \) の露点温度といえます。
したがって、\( T_1\) は「仮温度」ではなく「露点温度」が正解です。
(この時点でこの問題は 誤 であると判断できます。)
ちなみに、仮温度とは、湿潤空気と同圧・同密度の乾燥空気がもつべき仮想的な温度のことです。
また、温度 \( T_2 \) は、湿球を通過した後の温度で、この温度を湿球温度計が計測するので、正解は湿球温度です。
まとめると、\( T_2 \) は湿球温度で正しいですが、
\( T_1 \) は仮温度ではなく、露点温度であるため、答えは 誤 となります。
本問の解説:(b) について
(b) 湿球温度計に通風される未飽和空気(乾球温度\(T_0\) )の露点温度を \(T_1\)、湿球を通過した空気の湿球温度を \(T_2\) とするとき、 (b) \(T_1 < T_2\) である。
→ これは 正 です。
湿球温度計に通風される未飽和空気塊 \( \text{A} \) (乾球温度 \(T_0\)、混合比 \(W_1\)、露点温度 \(T_1\))と、湿球を通過した空気塊 \( \text{B} \) (湿球温度 \(T_2\)、混合比 \(W_2\)、露点温度 \(T_3\))をプロットすると下図のようになります。
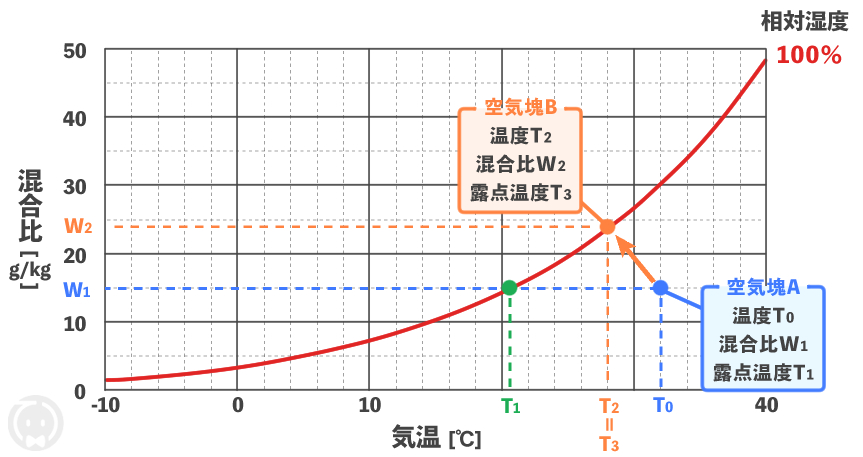




上の図を見ながら一緒に考えてみよう!
空気塊 \( \text{B} \) の混合比 \(W_2\) は、湿球を通過して水蒸気質量が空気塊 \( \text{A} \) の混合比 \(W_1\) より増えているので \( W_1 < W_2\) となります。
\( W_1 < W_2\) より、空気塊 \( \text{B} \) の露点温度 \(T_3\) は空気塊 \( \text{A} \)の露点温度 \(T_1\) より高く、\(T_1 < T_3\) となります。
また、空気塊 \( \text{B} \) は濡れたガーゼにより相対湿度100%ですので、湿球温度 \(T_2\) と露点温度 \(T_3\) は等しく、\(T_2 = T_3\)となります。
さらに、空気塊 \( \text{B} \) の湿球温度 \(T_2\) は、濡れたガーゼから気化熱(蒸発熱)を奪われて、空気塊 \( \text{A} \) の乾球温度 \(T_0\) より低くなっているので \( T_2 < T_0\) となります。
したがって、\(T_1 < T_2 = T_3 < T_0 \) という関係式が成り立つので、\(T_1 < T_2\) であり、答えは 正 となります。
本問の解説:(c) について
(c) 混合比の差 \( \Delta W = W_2\ – W_1\) に相当する水の蒸発によって温度が変化していることから、蒸発の潜熱を \(L\) 、定圧比熟を\(C_p\) とすれば、 (c) \(L \Delta W = C_p ( T_0\ – T_2 ) \) という関係が成り立つ。
→ これは 正 です。





まずは左辺から考えてみよう!
蒸発の潜熱 \( L \) とは、単位質量(1kg)の水が水蒸気に蒸発するために必要なエネルギー [J kg-1] のことです。
混合比 \( W_1, W_2 \) とは、湿潤空気に含まれる「水蒸気の質量」と「乾燥空気の質量」の比のことです。
混合比の差 \( \Delta W = W_2\ – W_1 \) とは、濡れたガーゼを通って増えた水蒸気の割合ことです。
蒸発の潜熱 \( L \) だけでは、濡れたガーゼの水がどれくらいエネルギーを奪って蒸発するのかわかりません。
そこで、\(W_1\) から \(W_2\) の間でどれだけ水蒸気が増えたかを表す「混合比の差 \( \Delta W = W_2\ – W_1\) 」を掛けることで、濡れたガーゼの水がどれくらいエネルギーを奪って蒸発するのかを表すことができます。
つまり「蒸発の潜熱 \( L \)」と「混合比の差 \( \Delta W \)」の積 (\( L × \Delta W\)) は、\(W_1\) から \(W_2\) の間で増えた水を水蒸気に蒸発させるのに必要なエネルギーということです。



次は右辺を考えてみよう!
定圧比熱 \(C_p\) とは、圧力一定下において、単位質量当たり、1K上昇させるのに必要なエネルギー [J kg-1 K-1] のことです。
定圧比熱 \(C_p\) と気温の差 \(T_0\ – T_2 \) の積( \( C_p ( T_0\ – T_2 ) \) ) は、圧力一定下において、単位質量当たり、乾球温度と湿球温度の差\(T_0\ – T_2 \)[K]上昇させるのに必要なエネルギー [J kg-1] を表します。
つまり、\( W_1 \) から \( W_2 \) で増えた水を水蒸気に蒸発させるのに必要なエネルギーは、圧力一定下において、単位質量当たり、\(T_0\ – T_2 \)[K]上昇させるのに必要なエネルギーと等しくなるので、左辺と右辺は等しくなります。



む、難しい・・・



もっと簡単に言うと、気温を (\(T_0\ – T_2 \)) [K] 上げるのに必要な蒸発の潜熱が \( L × \Delta W\) [J kg-1] っていうことだよ!
したがって、\(L \Delta W = C_p ( T_0\ – T_2 ) \) という等式が成り立つので、答えは 正 となります。
以上より、本問の解答は (a) 誤 (b) 正 (c) 正 とする 3 となります。
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。




コメント