問7
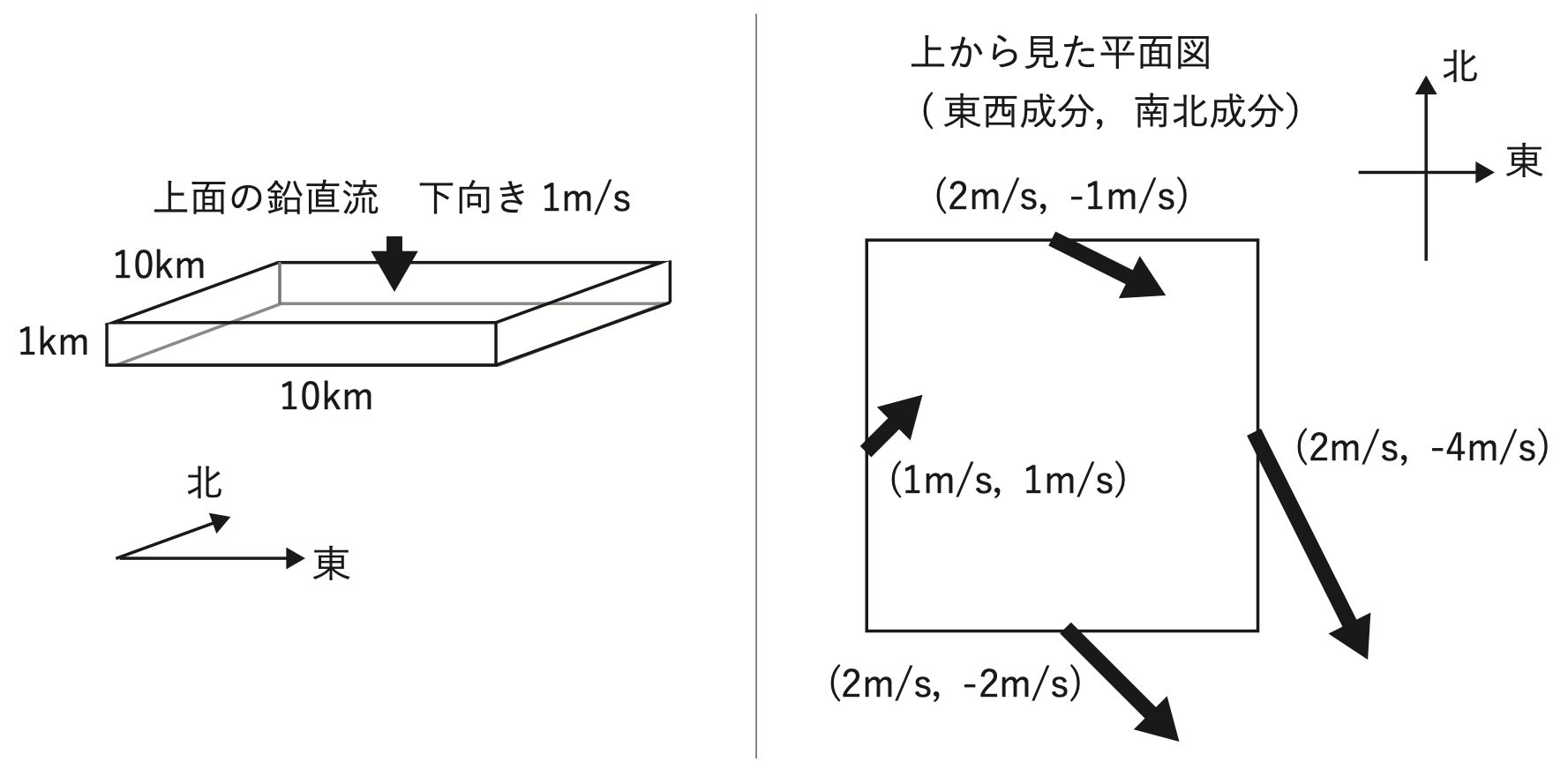
大気中に図 (左) のような高さが1km、東西および南北方向の長さが10kmで、4つの側面がそれぞれ東西南北を向いた直方体の領域があり、上面からは下向きに1m/sの鉛直流が、また東西南北の各側面には図 (右) の ( ) に示す東向きを正とする東西成分、北向きを正とする南北成分の水平風が、いずれも各面に一様に吹いている。
この領域の底面で一様に吹いていると仮定した場合の鉛直流の向き及び大きさと、領域で平均した渦度の鉛直成分の組み合わせとして正しいものを、下記の1~5の中から1つ選べ。ただし、空気の密度は一定であり、渦度の鉛直成分は上向きを正とする。
本問は、鉛直流と渦度に関する計算問題です。
本問の解説:(底面の鉛直流) について
(問題)大気中に図 (左) のような高さが1km、東西および南北方向の長さが10kmで、4つの側面がそれぞれ東西南北を向いた直方体の領域があり、上面からは下向きに1m/sの鉛直流が、また東西南北の各側面には図 (右) の ( ) に示す東向きを正とする東西成分、北向きを正とする南北成分の水平風が、いずれも各面に一様に吹いている。
この領域の底面で一様に吹いていると仮定した場合の鉛直流の向き及び大きさを求めよ。ただし、空気の密度は一定であり、渦度の鉛直成分は上向きを正とする。

→ 答えは 下向き0.8m/s です。
まず、問題文に「空気の密度は一定」との条件がありますので、直方体への空気の流入、流出があっても、直方体全体の空気の質量は一定となります(=保存されます)。
つまり、直方体の上面と側面からの流入量の合計が、底面での流出量と等しくなります。
この、底面での流出量が、求めたい底面の鉛直流というわけです。
ある平面を通して単位時間あたりに流入する空気量Mは、
空気の密度をρ、平面の面積をS、平面に直交する風の成分をνとすると
M (g/s) = ν(m/s) ρ(g/m3) S(m2)
と求めることができます(νは直方体に流入する向きを正とする)。
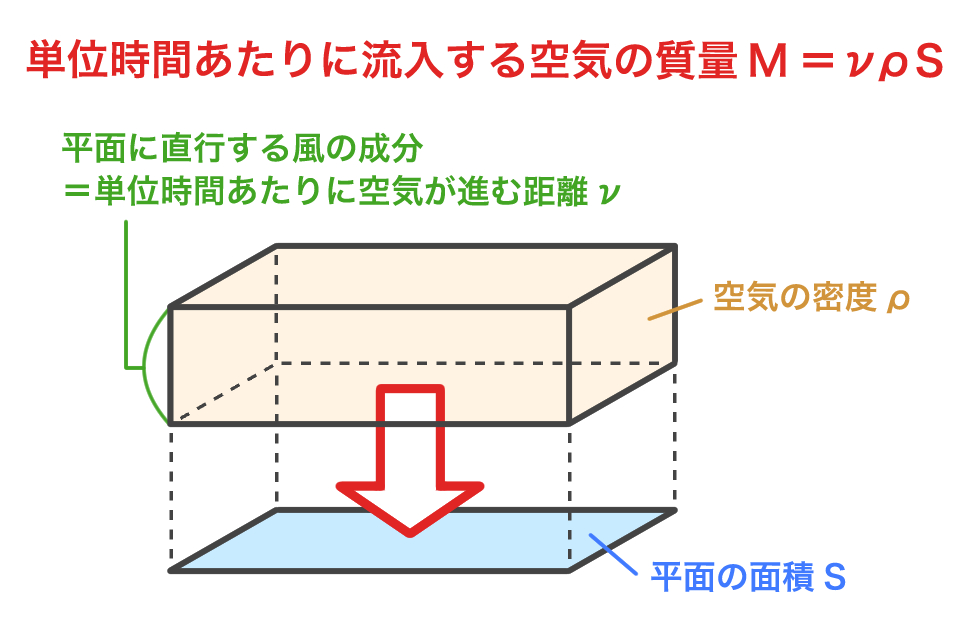
Mの単位は (g/s) ですので、Mは、ある平面に向かって、単位時間あたりに何グラムの空気が流入しているか、ということを表しています。
では、本問の計算をしてみましょう。
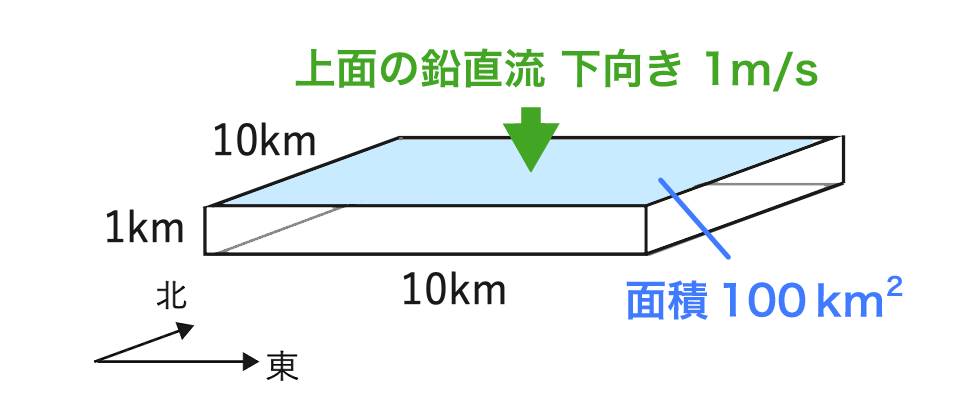
上面は、面積 100 (km2) に向かって1(m/s) の空気が流入していますので、空気の密度をρ(g/m3) とすると、上面からの空気の流入量は
上面からの流入量
= 1(m/s) × ρ (g/m3) × 100 (km2)
= 100ρ (kg/s)
上面からの流入量 = 1(m/s) × ρ (g/m3) × 100 (km2) = 100ρ (kg/s)
となります。
次は、側面からの空気の流入量を考えてみましょう。
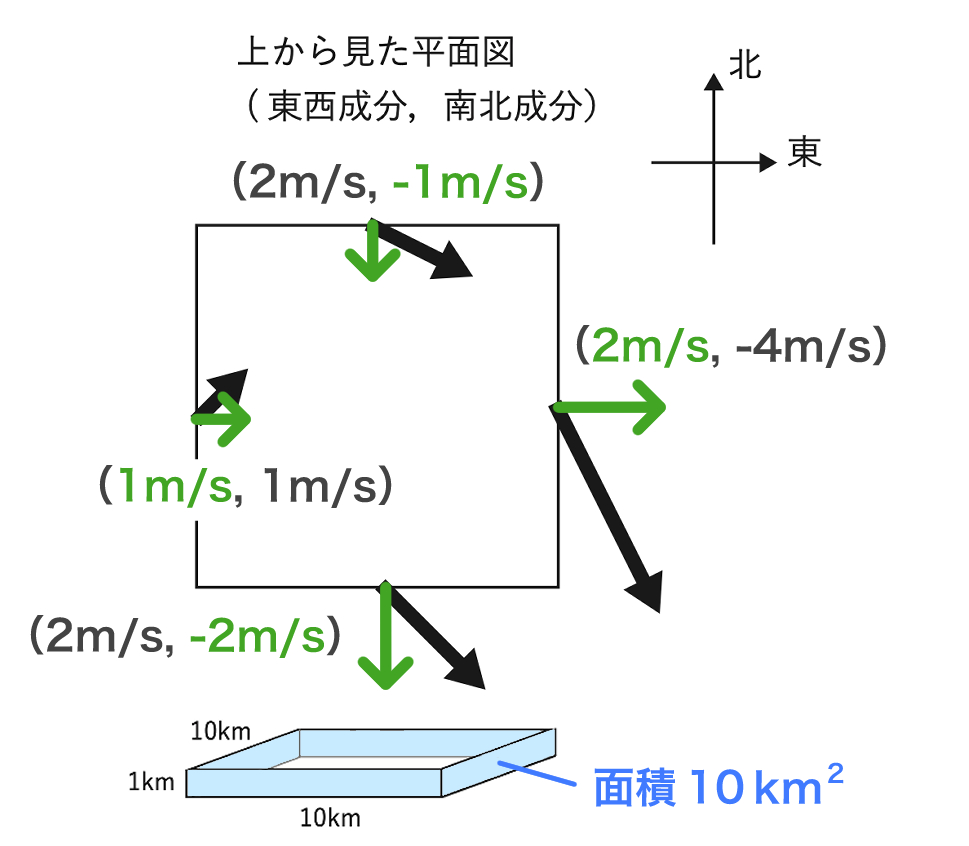
北側面は、面積 S = 10 (km2) に向かって1(m/s) の空気が流入しています(=流入する向きを正)ので、北側面からの空気の流入量は
北側面からの流入量
= 1(m/s) × ρ(g/m3) × 10 (km2)
= 10ρ (kg/s)
北側面からの流入量 = 1(m/s) × ρ(g/m3) × 10 (km2) = 10ρ (kg/s)
となります。
同様に、東側面、南側面、西側面から立方体に向かって直角に流入する風の成分は、流入する向きを正とすると
東側面:東西成分 (-2(m/s))
南側面:南北成分 (-2(m/s))
西側面:東西成分 (1(m/s))
であり、面積はすべて S = 10 (km2) ですので
東側面からの流入量
= -2(m/s) × ρ (g/m3) × 10 (km2)
= -20ρ (kg/s)
南側面からの流入量
= -2(m/s) × ρ (g/m3) × 10 (km2)
= -20ρ (kg/s)
西側面からの流入量
= 1(m/s) × ρ (g/m3) × 10 (km2)
= 10ρ (kg/s)
東側面からの流入量 = -2(m/s) × ρ (g/m3) × 10 (km2) = -20ρ (kg/s)
南側面からの流入量 = -2(m/s) × ρ (g/m3) × 10 (km2) = -20ρ (kg/s)
西側面からの流入量 = 1(m/s) × ρ (g/m3) × 10 (km2) = 10ρ (kg/s)
となります。
上面および側面からの全流入量は、これらを合計して
全流入量
= 100ρ + 10ρ - 20ρ - 20ρ + 10ρ
= 80ρ
全流入量 = 100ρ + 10ρ - 20ρ - 20ρ + 10ρ = 80ρ
となります。
問題文より「空気の密度は一定」ですので、この全流入量が、底面からの流出量と等しくなります。
したがって、底面全体からの流出量が -80ρ ですので、底面の鉛直流 (下降流) の大きさは、
これを底面の面積 100 (km2) と密度 ρ で割り算すれば
底面の鉛直流 (下向き)
= -80ρ(kg/s) / 100ρ(km2 g/m3)
= -0.8 (m/s)
底面の鉛直流 (下向き) = -80ρ(kg/s) / 100ρ(km2 g/m3) = -0.8 (m/s)
となりますので、
答えは 下向き0.8m/s となります。
本問の解説:(渦度の鉛直成分) について
(問題)大気中に図 (左) のような高さが1km、東西および南北方向の長さが10kmで、4つの側面がそれぞれ東西南北を向いた直方体の領域があり、上面からは下向きに1m/sの鉛直流が、また東西南北の各側面には図 (右) の ( ) に示す東向きを正とする東西成分、北向きを正とする南北成分の水平風が、いずれも各面に一様に吹いている。
この領域の底面で一様に吹いていると仮定した場合の、領域で平均した渦度の鉛直成分を求めよ。ただし、空気の密度は一定であり、渦度の鉛直成分は上向きを正とする。

→ 答えは -5×10-4/s です。
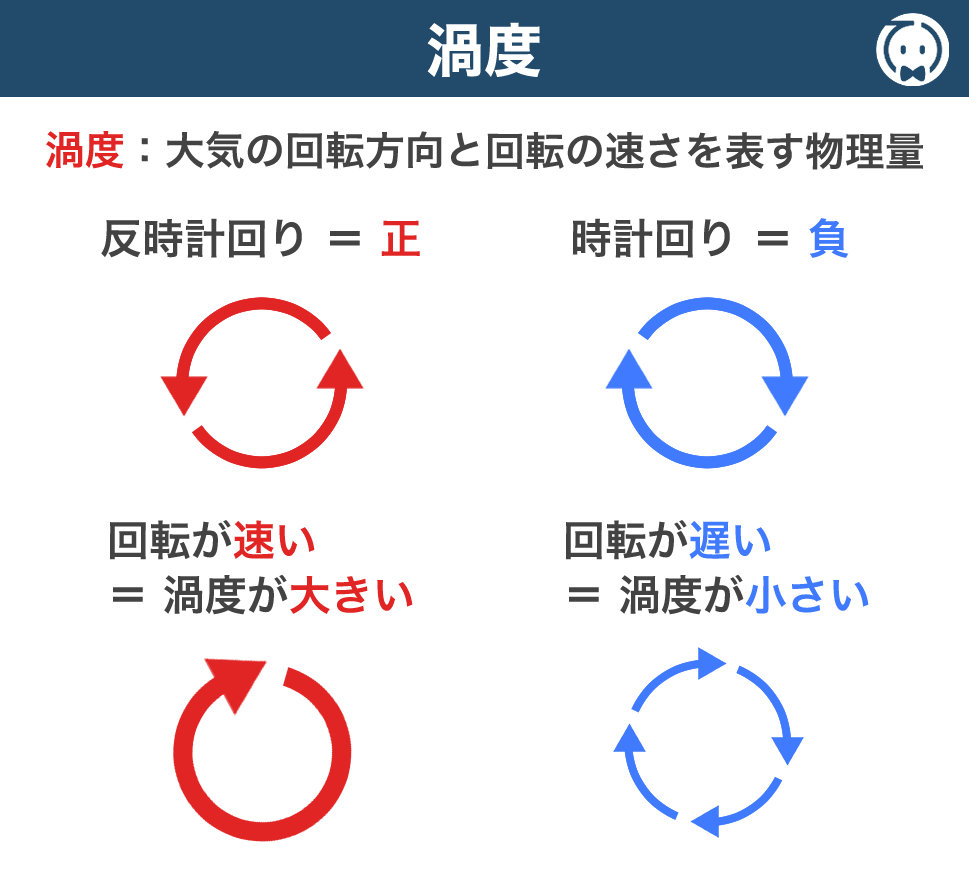
渦度(読:うずど)とは、大気の回転方向と回転の速さを表す物理量です。
大気の流れはまっすぐ進むものだけではなく、回転しているものもあります。
この回転している状態を表すものが渦度です。
また、回転方向には、反時計回り(正)と時計回り(負)があり、
回転が速いほど、渦度が大きいと表現します。
では、なぜ気象学では、渦度が重要なのでしょうか?
それは、渦度が低気圧や高気圧といった大規模な気象現象と関係しているからです。
例えば、渦度を使うことで、低気圧や高気圧の位置、上昇流や下降流の位置、天気の変化などを予測することができます。
さらに、負の渦度は高気圧やリッジに、正の渦度は低気圧やトラフに対応しており、これが上層大気の蛇行や上昇・下降流と密接に関係しています。
一般に、気象学で渦度というときは、相対渦度の鉛直成分 のことをいいます。
相対渦度 とは、地面との相対的な意味での渦という意味であり、
対して、地球の外から地球上の渦をみたものを絶対渦度といいます。
本問で求める「渦度の鉛直成分」も「相対渦度の鉛直成分」を求めますので、
以降、「渦度」は「相対渦度」、「渦度の鉛直成分」は「相対渦度の鉛直成分」のことを表します。
 てるるん
てるるんここはちょっと難しいから、詳しく理解したい人は読んでみてね!
分からない人は読み飛ばして大丈夫だよ!
気象学で一般に 渦度 というときには、渦度の鉛直成分 のことをいいます。
では、なぜ「渦度」=「渦度の鉛直成分」なのでしょうか?
大気は3次元上に存在しますので、大気の回転も3次元で表現する必要があります。
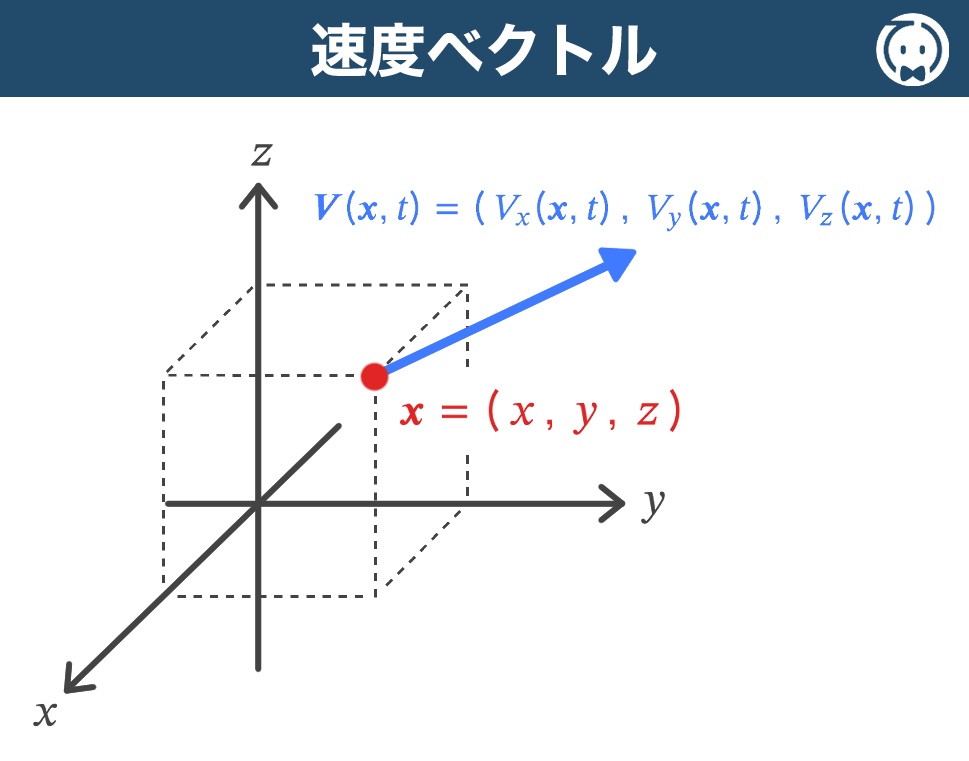

そこで、ある領域内の点を
\( \boldsymbol{x} = (\, x\, , \, y\, , \, z\, ) \) とし、
時刻 \( t \) における流体の速度ベクトルを
\( \boldsymbol{V}(\boldsymbol{x}, t) = (\, V_x(\boldsymbol{x}, t)\, , \, V_y(\boldsymbol{x}, t)\, , \, V_z(\boldsymbol{x}, t)\, ) \)
とすると、
時刻 \( t \) における流体の速度ベクトルを\( \boldsymbol{V}(\boldsymbol{x}, t) = (\, V_x(\boldsymbol{x}, t)\, , \, V_y(\boldsymbol{x}, t)\, , \, V_z(\boldsymbol{x}, t)\, ) \)とすると、
渦度 \( \boldsymbol{\zeta} \) (読:ゼータ) は速度場の回転( \( \text{rot} = \nabla \times \) )を使って
\begin{align} \displaystyle \boldsymbol{\zeta} &= \nabla \times \boldsymbol{V} \\&=
\left(
\frac{\partial V_z}{\partial y}\; – \, \frac{\partial V_y}{\partial z}\, , \,
\frac{\partial V_x}{\partial z}\; – \, \frac{\partial V_z}{\partial x}\, , \,
\frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y}
\right) \tag{1} \end{align}
\( \displaystyle \boldsymbol{\zeta} = \nabla \times \boldsymbol{V} =
\left(
\frac{\partial V_z}{\partial y}\; – \, \frac{\partial V_y}{\partial z}\, , \,
\frac{\partial V_x}{\partial z}\; – \, \frac{\partial V_z}{\partial x}\, , \,
\frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y}
\right) \tag{1}\)
と定義されます。



速度場の回転( \( \text{rot} = \nabla \times \) )については、ヨビノリさんの動画が分かりやすかったよ!
(1)式のとおり、大気の回転は3次元の現象なので、本来、渦度は3次元で考えるべきものです。
しかし、気象学において、総観規模スケールの現象を扱う際には静力学平衡が成り立ち、
鉛直方向(= \( z \) 軸方向)の速度は水平方向の速度と比較して極めて小さくなりますので、
鉛直方向(= \( z \) 軸方向)の動きは無視することができます。
つまり、(1)式において、 \( z \) のつく項がすべて0になりますので、
渦度 \( \boldsymbol{\zeta} \) は、以下のように表すことができます。
\( \displaystyle \boldsymbol{\zeta} = \nabla \times \boldsymbol{V} =
\left(
0\, , \,
0\, , \,
\frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y}
\right) \tag{2}\)
\( \displaystyle \boldsymbol{\zeta} = \nabla \times \boldsymbol{V} =
\left(
0\, , \,
0\, , \,
\frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y}
\right) \tag{2}\)
この(2)式は、静力学平衡が成り立つと仮定した場合、大気の回転(=渦度)は \( z \) 軸周りでの回転(= \( x, y \) 平面上での回転 )のみ生じる、ということを意味しています。
そして、この \( z \) 軸周りでの回転が、渦度 \( \boldsymbol{\zeta} \) の \( z \) 軸成分(=鉛直成分)となりますので、渦度の鉛直成分は以下のようになります。
渦度の鉛直成分 = \( \displaystyle \frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y} \)
渦度の鉛直成分 = \( \displaystyle \frac{\partial V_y}{\partial x}\; – \, \frac{\partial V_x}{\partial y} \)
したがって、気象学において一般に渦度とは、
静力学平衡が成り立つと仮定した場合の渦度 \( \boldsymbol{\zeta} \) であり、
渦度 \( \boldsymbol{\zeta} \) の \( z \) 成分 (=\( z \) 軸周りでの回転 = 鉛直成分)を考えますので、
「渦度」=「渦度の鉛直成分」というわけです。
渦度の鉛直成分は、下記の式で表すことができます。
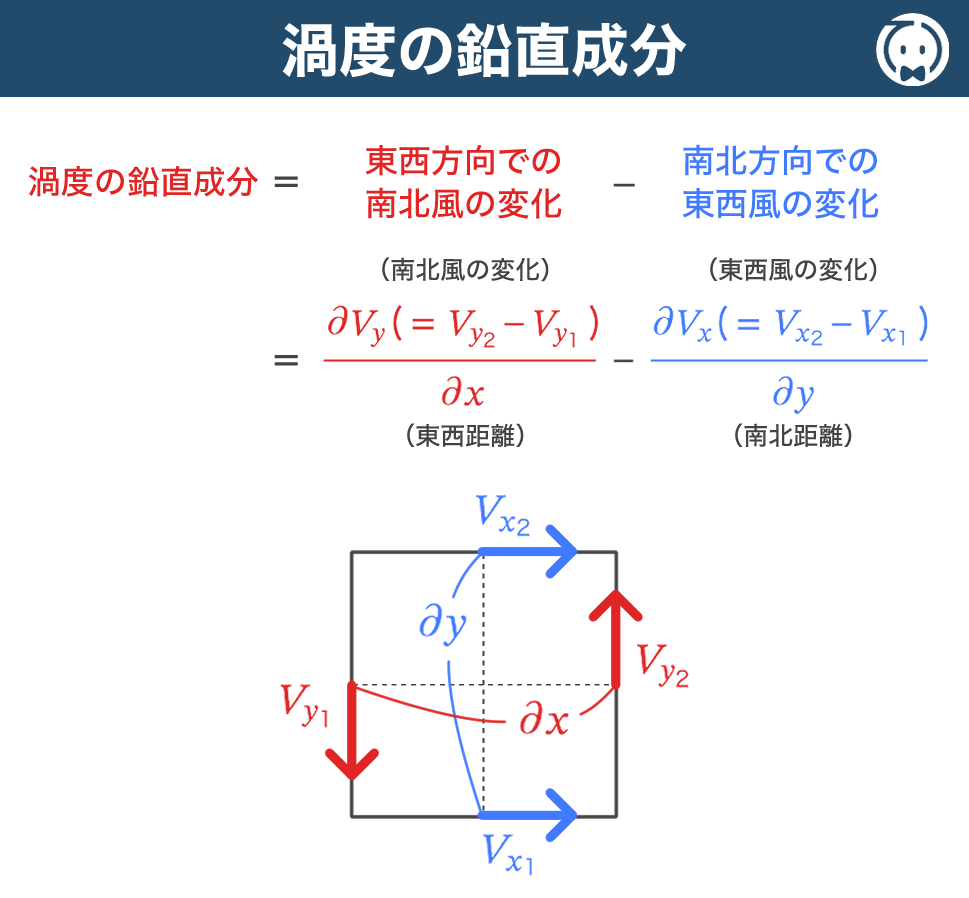

この式は、ざっくり説明すると
東西方向での南北風の変化と、南北方向での東西風の変化から、相対渦度の鉛直成分を求めています。
① 東西方向での南北風の変化
これは、南北方向の風速が、東西方向でどう変化するかを求めます。
例えば、東に行くほど北風が強くなる場合、渦は反時計回りになりますので、渦度は正になります。
また、東西方向で南北の風速差が大きくなる場合、渦の回転が速くなりますので、渦度が大きくなります。
② 南北方向での東西風の変化
これは、東西方向の風速が、南北方向でどう変化するかを求めます。
例えば、北に行くほど西風が強くなる場合、渦は時計回りになりますので、渦度は負になります。
また、南北方向で東西の風速差が小さくなる場合、渦の回転が遅くなりますので、渦度が小さくなります。
したがって、① 東西方向での南北風の変化と、② 南北方向での東西風の変化 から、相対渦度の鉛直成分を求めることができるというわけです。
では、本問を解いてみましょう。
① 東西方向での南北風の変化
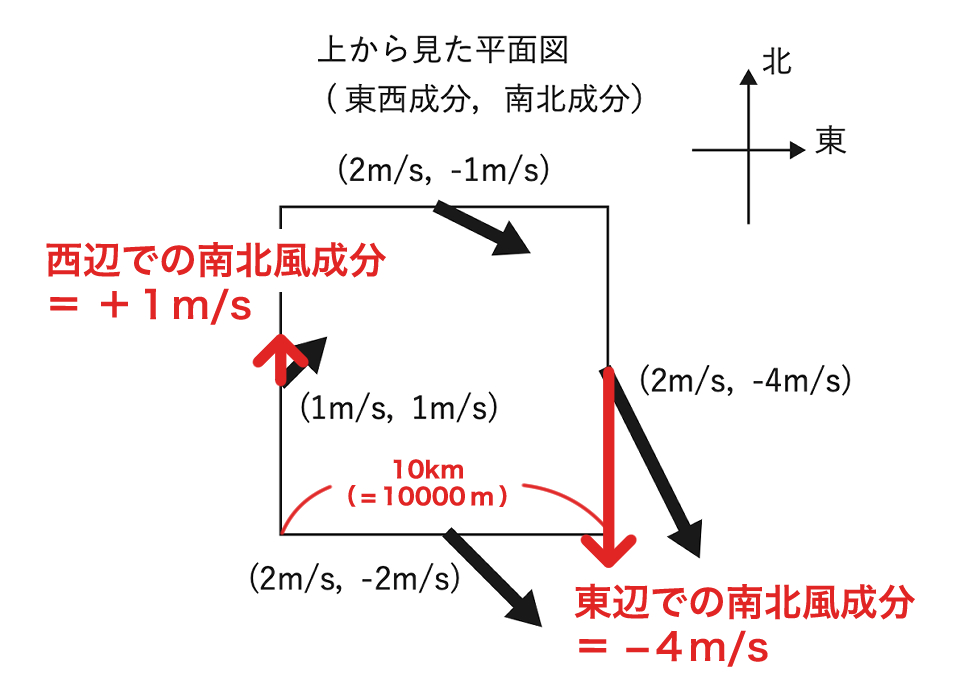

北向きを正(=南風が「+」、北風が「−」)とすると、
東辺での南北風成分は−4m/s、西辺での南北風成分は+1m/sですので、
風速差は −4−(+1) = −5m/s となります。
また、西辺と東辺の距離は10km(=10000m)です。
したがって、東西方向での南北風の変化は
東西方向での南北風の変化
= \( \displaystyle \,\frac{- \; 5}{\; 10000\quad} \)
= −5×10-4/s
東西方向での南北風の変化 = \( \displaystyle \,\frac{- \; 5}{\; 10000\quad} \) = −5×10-4/s
となります。
② 南北方向での東西風の変化
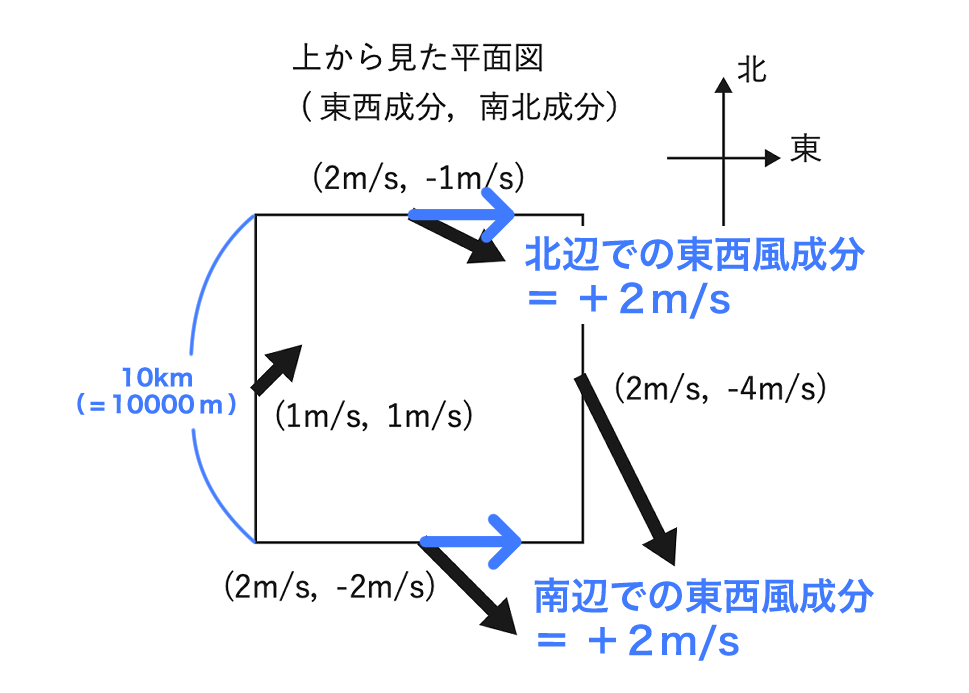

東向きを正(=西風が「+」、東風が「−」)とすると、
北辺での東西風成分は+2m/s、南辺での東西風成分は+2m/sですので、
風速差は +2−(+2) = 0m/s となります。
また、北辺と南辺の距離は10km(=10000m)です。
したがって、南北方向での東西風の変化は
南北方向での東西風の変化
= \( \displaystyle \,\frac{0}{\; 10000\quad} \)
= 0/s
南北方向での東西風の変化 = \( \displaystyle \,\frac{0}{\; 10000\quad} \) = 0/s
となります。
したがって求める渦度の鉛直成分は
渦度の鉛直成分
= −5×10-4 −0
= −5×10-4/s
渦度の鉛直成分 = −5×10-4 −0 = −5×10-4/s
となります。
以上より、本問の解答は
(底面の鉛直流) 下向き0.8m/s
(渦度の鉛直成分) -5×10-4/s
とする 5 となります。
書いてある場所:P163〜165(渦度)
書いてある場所:P339〜344(渦度)
書いてある場所:P270〜275(渦度)
書いてある場所:P207〜210(渦度)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。





コメント
コメント一覧 (4件)
おとといはコメント欄がなかったので、問い合わせから送ったんですが、
コメント欄ができた(?)ので、こっちにも送っておきます。
—
「渦度の鉛直成分」の図について
矢印の向きはヨビノリの動画に合わせてあると思うのですが、
動画のコメント欄でも指摘のあるように、矢印の向きが統一されてないように思います。
・Vy1 を逆にする(座標軸に着目)
かあるいは、
・Vx2 を逆にする(渦度に着目)
方がいいと思います。
個人的な直感では Vx2 を逆にするほうが自然かなと思いましたが、
コメント欄では Vy1 を逆にすべきという意見が多かったようです。
—
V の意味を考えると、Vy1 を逆(上向き)にしたほうがいいかもしれませんね。
cs様
コメントありがとうございます。
矢印の向きにつきましては、ヨビノリさんの動画だけでなく、
「一般気象学」(著:小倉義光)の164ページ目、または
「イラスト図解 よくわかる気象学 第2版」(著:中島俊夫)の280ページ目に
本ブログで使用した「渦度の鉛直成分」の図と同じ図が掲載されております。
したがって、「渦度の鉛直成分」の図の矢印の向きは問題ないと考えます。
では、なぜこのような矢印の向きで表示しているかというと、
渦度の解析は、基本的に500hPa付近で行うためだと考えます。
上空500hPaにもなると、日本の上空(=中緯度帯)では偏西風が吹いています。
したがって、日本の上空の大気を簡易的に表すための図が「渦度の鉛直成分」の図であり、
Vx1とVx2はどちらも西風で表現しているのだと思います。
一方、偏西風の蛇行により南北風は変化しますので
Vy1は北風、Vy2は南風で表現しているのだと思います。
よろしくお願いいたします。
>一方、偏西風の蛇行により南北風は変化しますので
>Vy1は北風、Vy2は南風で表現しているのだと思います。
これが理由だとしたら、考えている ∂x はけっこう距離が長く、微小とは言えないと思いませんか?
cs様
コメントありがとうございます。
ヨビノリさんの動画のコメント欄にもあるように、
矢印の向きに必ずこうしなければならないという決まりはありませんので、
たしかにcs様のような考え方もできるかもしれません。
— ヨビノリさんの動画のコメント欄 —————–
Q.なんで下向きのベクトルを書いたの?(4:16)
A.板の周りに描いてあるベクトルの向きに意味はなく、適当に描いたものです。例えばこのとき描いたベクトルは負の成分をもつベクトルであると解釈されます。
——————————————
より正確な回答をお望みでしたら、出版社等にお尋ねいただく方が正確かと思います。
よろしくお願いいたします。