問3
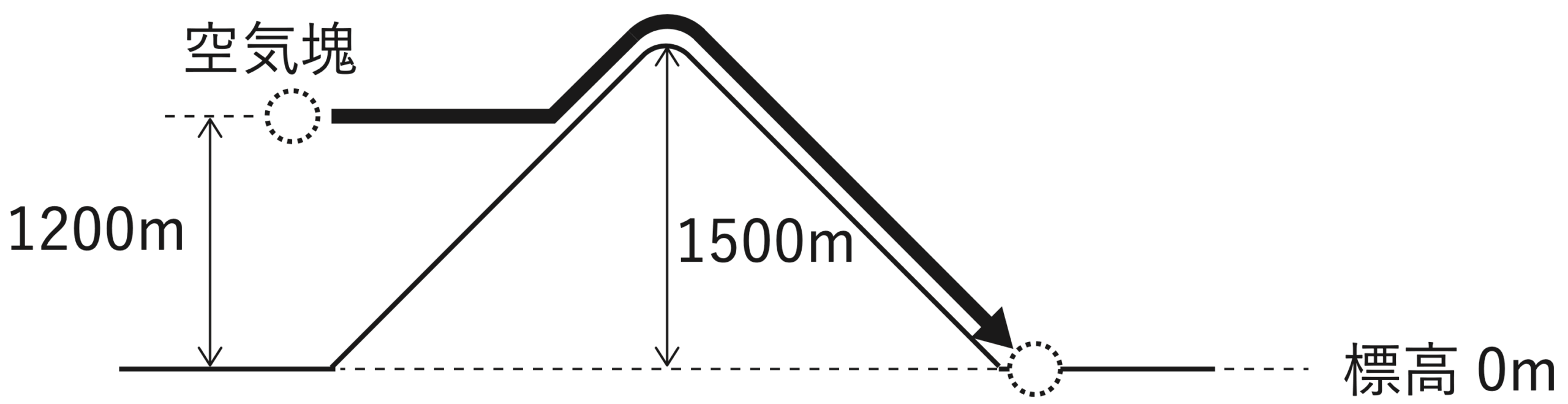
図に示すように、標高0m の平野にある標高 1500m の山を考える。大気はどこでも気温減率が6℃/km で、標高0mの気温は 30℃ である。このとき、山の左側の高度 1200m の微小な空気塊を、山を越えて右側の標高0m の麓まで、周囲と混合しないように断熱的に下降させた。この下降後の空気塊の温度に最も近いものを、下記の1~5の中から1つ選べ。ただし、空気塊の移動中に水蒸気の凝結は起こらないものとする。
本問は、フェーン現象に関する計算問題です。
本問の解説
(問題)図に示すように、標高0m の平野にある標高 1500m の山を考える。大気はどこでも気温減率が6℃/km で、標高0mの気温は 30℃ である。このとき、山の左側の高度 1200m の微小な空気塊を、山を越えて右側の標高0m の麓まで、周囲と混合しないように断熱的に下降させた。この下降後の空気塊の温度に最も近いものを、下記の1~5の中から1つ選べ。ただし、空気塊の移動中に水蒸気の凝結は起こらないものとする。

→ 答えは 34.8℃ です。
湿潤な空気が山を越えて反対側に吹き下りたときに、風下側で吹く乾燥した高温の風のことを フェーン といい、 そのために付近の気温が上昇することを フェーン現象 といいます。
フェーン現象に関する計算問題の基本的な解き方の流れは以下の通りです。
① 初期位置での温度を求める
② 山頂までの温度変化を求める
③ 麓までの温度変化を求める
では、具体的に計算してみましょう。
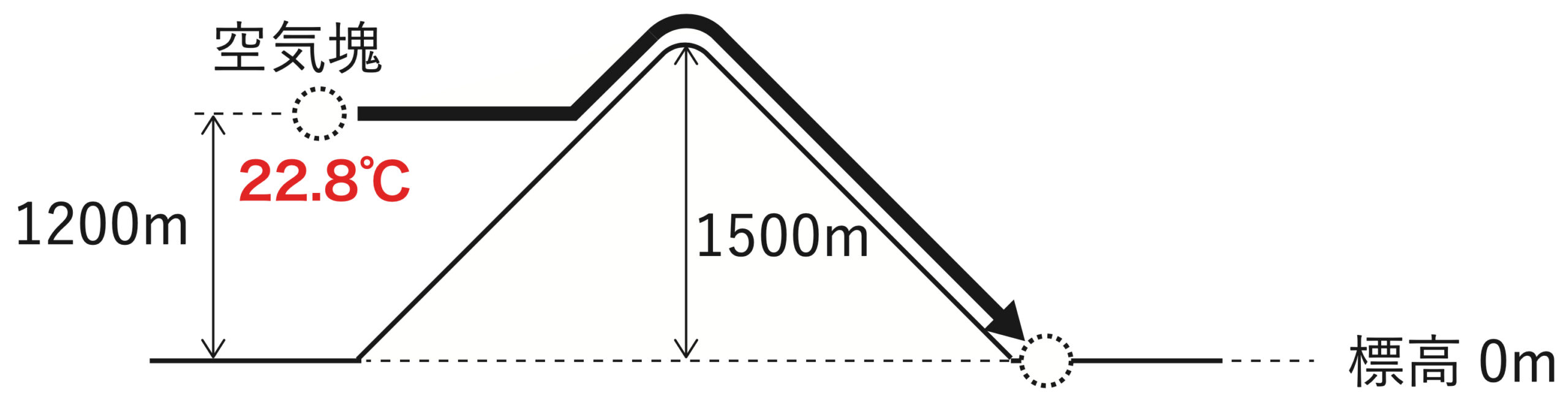
① 初期位置(高度 1,200m)での温度を求める
空気塊は山の左側の高度 1,200m にあり、その温度は周囲の大気の気温と同じと考えます。
標高0mの気温は 30℃ で、大気の気温減率は6℃/km なので、高度 1200m の空気塊の温度は
30 [℃] − 6[℃/km] × 1.2 [km] = 22.8 [℃]
となります。
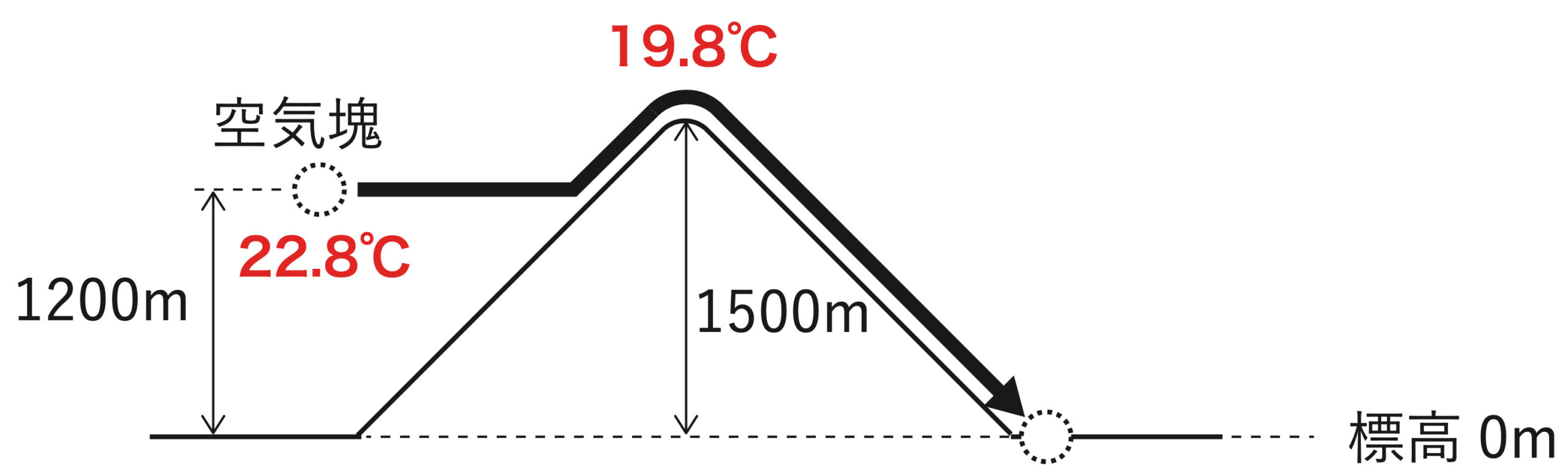
② 山頂(標高 1,500m)までの温度変化を求める
山頂までは水蒸気の凝結は起きないので、乾燥断熱減率(10℃/km)を使います。
空気塊が上昇する高さは 300m(高度 1,200m → 1,500m へ上昇)なので、その冷却量は
10 [℃/km] × 0.3 [km] = 3.0 [℃]
となります。
つまり、山頂での温度は
22.8 [℃] − 3.0 [℃] = 19.8 [℃]
となります。
③ 麓(標高0m)までの温度変化を求める
山頂で水蒸気は凝結していないので、乾燥断熱減率(10℃/km)を使います。
空気塊が下降する高さは 1,500m(高度 1,500m → 0m へ下降)なので、その加熱量は
10 [℃/km] × 1.5 [km] = 15.0 [℃]
となります。
つまり、麓での温度は
19.8 [℃] + 15.0 [℃] = 34.8 [℃]
となります。
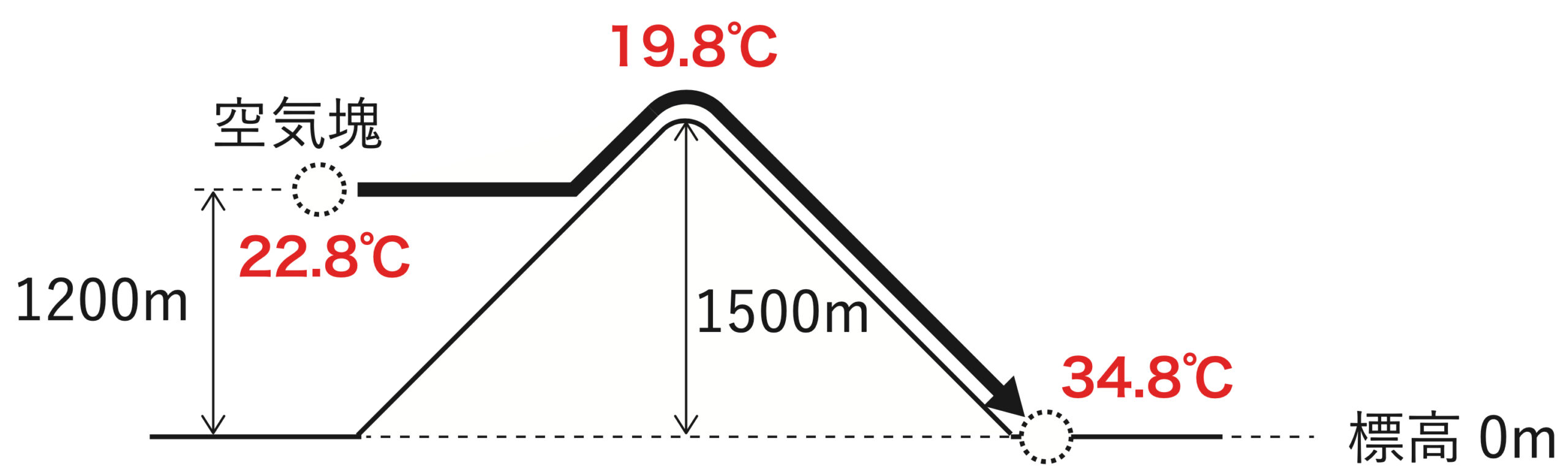
したがって、高度 1200m の微小な空気塊を、山を越えて右側の標高0m の麓まで、周囲と混合しないように断熱的に下降させたときの温度は 34.8℃ なので、答えは 4 となります。
書いてある場所:ー
書いてある場所:P109〜110(フェーン現象)
書いてある場所:P64〜65(フェーン現象)、P134(湿ったフェーンと乾いたフェーン)
書いてある場所:P148〜150(フェーン)
書いてある場所:P328〜344(気象関連法令集)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。








コメント