【第63回】2025年１月試験（学科一般試験）問７（収束・発散・鉛直流）

本問は、連続の式（質量保存則）を用いて、３つの直方体を通過する空気の収束量から直方体上端の上昇流を求める問題です。

本問の解説

（問題）図のように、地表面から鉛直に重なった高さ H、H、２H の３つの直方体の領域を考える。各直方体の東側と西側の面では、図に示す西風が各面内で一様に吹いている。各直方体の南側と北側の面を通過する風はなく、地表面以外の水平面 A、B、C では鉛直風が各面内で一様に吹いている。面 A における鉛直風速が上向きを正として 0.5m/s であるとき、面 C における鉛直風速として正しいものを、下記の１～５の中から１つ選べ。ただし、大気の密度はどこも同じで一定とする。

→ 答えは ４ の 0.5 m/s です。

収束・発散 D の近似計算式は下図のように表されます。

３次元の空気の流れにおける収束・発散 D の関係式は、空気が圧縮されたり膨張したりして密度が変わることも含めて、連続の式（質量保存の法則）と呼ばれています。

しかし、本問のように「大気の密度はどこも同じで一定」と仮定した場合は、空気の出入りの合計（つまり収束・発散の合計 D ）は０でなければなりません。

これは、空気の量（質量）が増えたり減ったりしないためです。

そのため、ある平面内で空気が収束して集まると、行き場を失った空気は上下、つまり鉛直方向に流れ出るしかありません。

逆に、空気が平面内で発散して広がっていく場合は、鉛直方向から空気が補われる必要があります。

よって、密度一定での質量保存則は

となります。

また、本問の設定では、南北面での流れがないため、V₁ = V₂ = ０ となり、

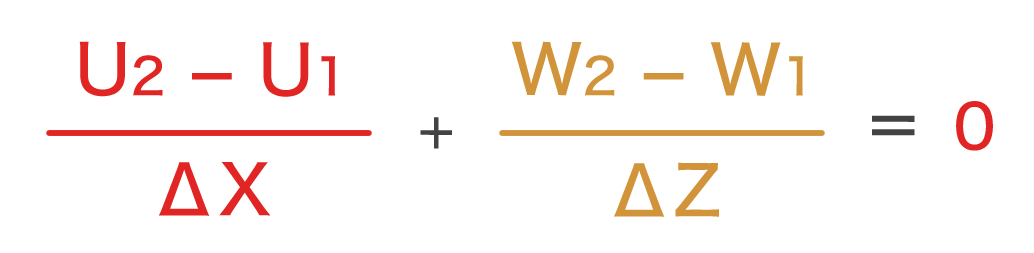
となります。

では、実際に問題を解いていきましょう。

最下層（地表面 ～ 面A）

まず、地表面から高さHまでの直方体（ 領域 0A ）について考えます。

この領域の東西風速は、西側で５ m/s、東側で４ m/sであり、西側からの流入が強いため、空気は収束しています。

また、地表面での鉛直風速 W₀ は W₀ = ０m/sであり、面 A での鉛直風速 W_A は、問題文より W_A = 0.5 m/s です。

直方体の東西方向の長さを ΔX として、これらを連続の式に当てはめると

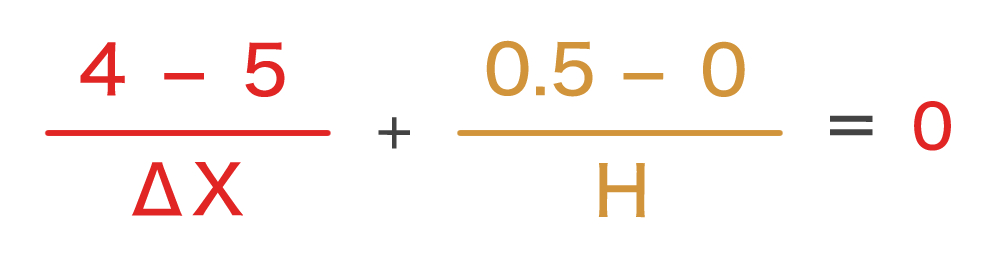
となり、この式を解くと、

ΔX = ２H　・・・（１）

となります。

中層（面A ～ 面B）

次に、H 〜２Hの高さにある直方体（ 領域 AB ）について考えます。

この領域の東西風速は、西側で５ m/s、東側で３ m/sであり、西側からの流入が強いため、空気は収束しています。

また、面 A での鉛直風速 W_A は、問題文より W_A = 0.5 m/s ですので、これらを用いて、面 B での鉛直風速 W_B を求めます。

直方体の東西方向の長さΔX は、（１）式より、ΔX = ２H なので、これらを連続の式に当てはめると

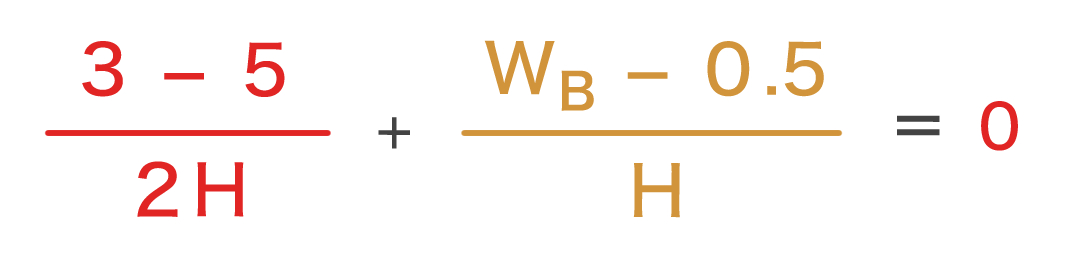
となり、この式を解くと、

W_B = 1.5 m/s　・・・（２）

となります。

最上層（面B ～ 面C）

最後に、２H 〜４Hの高さにある直方体（ 領域 BC ）を見てみます。

この領域の東西風速は、西側で４ m/s、東側で５ m/sであり、東側からの流出が強いため、空気は発散しています。

また、面 B での鉛直風速 W_B は（２）式より W_B = 1.5 m/s ですので、これらを用いて、面 C での鉛直風速 W_C を求めます。

直方体の東西方向の長さΔX は（１）式より、ΔX = ２H なので、これらを連続の式に当てはめると

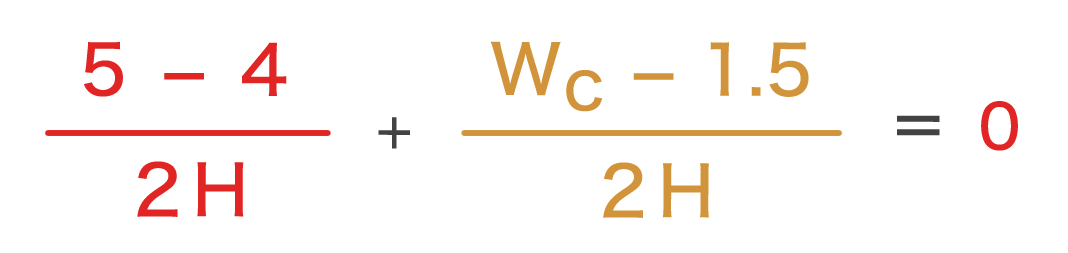
となり、この式を解くと、

W_C = 0.5 m/s

となります。

したがって、面 C における鉛直風速 W_C は 0.5 m/s となりますので、答えは ４ となります。