【第60回】2023年８月試験（学科専門試験）問５（数値予報モデル、CFL条件）

本問は、気象庁が行っている数値予報に関する問題です。

本問の解説：(a)について

（問題）数値予報モデルでは、連続的に変化する現実の大気の物理量を限られた数の格子点の値で代表しており、数値予報モデルで精度よく表現しうる現象は、水平スケールが格子間隔と同程度以上の現象である。

→ 答えは 誤 です。

数値予報モデル とは、大気の変化をコンピューターでシミュレーションするためのプログラムです。

しかし、すべての場所のデータを細かく取ることはできないので、格子点という特定の地点でのデータを使います。

ここで重要なのは、どれくらい細かくこの格子点を設定するかということです。

この間隔を 格子間隔 といいます。

では、気象現象の水平スケールと格子間隔の関係について考えてみましょう。

下図は、数値予報モデルの格子間隔と、現象の表現の関係を表しています。

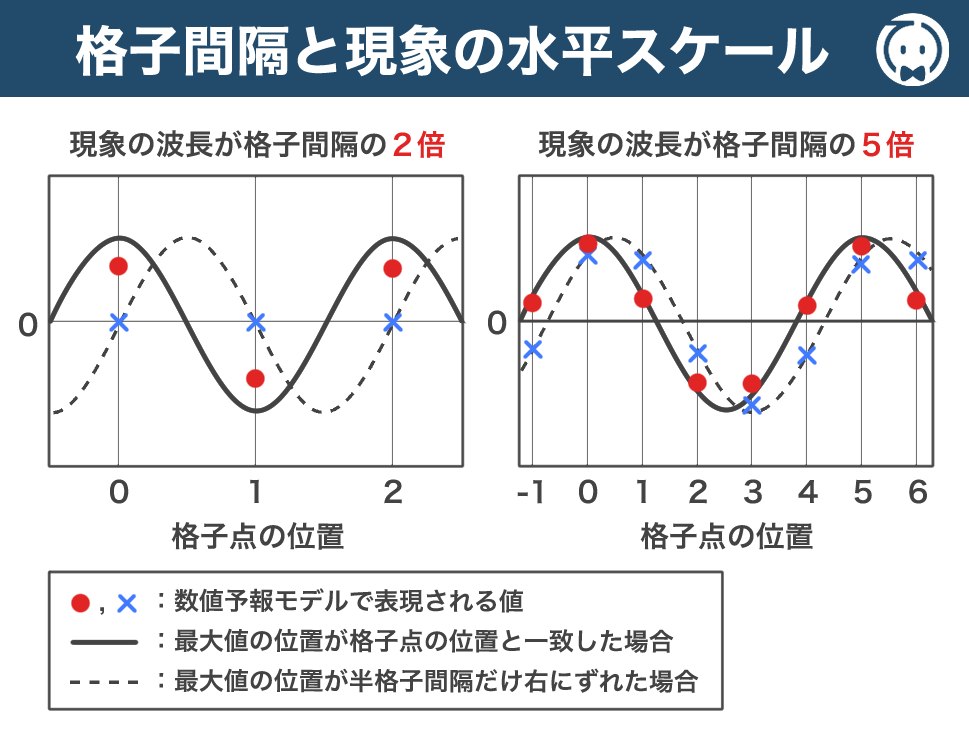
左図は、現象の波長が格子間隔の２倍で、

右図は、現象の波長が格子間隔の５倍となっています。

実線は、最大値の位置が格子点の位置と一致した場合を表し、

破線は、半格子間隔だけ右にずれた場合を表しています。

● と ✕ は、それぞれ数値予報モデルで表現される値です。

（注意点として、数値予報モデルの格子点の値は格子スケールで平均化されているため、元の値より振幅が小さくなります。）

左図は、現象の波長が格子間隔よりそこまで大きくないので、振幅が大幅に過小評価されるだけでなく、現象の位置によっては全く表現されないこともあり得ます。

一方、右図は、現象の波長が格子間隔より大きいので、現象の位置に関係なく比較的正確に表現されています。

これらの図は、現象の水平スケールが格子間隔よりある程度大きくないと、その現象を正しく表現できないことを表しています。

例えば、全球モデル（GSM）は格子間隔が約13kmですが、それより小さい波長（例：５kmや10km）の現象はこのモデルではうまく表現できません。

一方、波長が100kmくらい大きなスケールの現象は、比較的正確に表現されます。

経験的には、数値予報モデルが精度よく表現できる現象の水平スケールは、数値予報モデルの格子間隔の ５～８倍以上 とされています。

したがって、数値予報モデルで精度よく表現しうる現象は、「水平スケールが格子間隔と同程度以上の現象」ではなく、「格子間隔の５～８倍以上」とされていますので、答えは 誤 となります。

本問の解説：(b)について

（問題）積乱雲のような水平スケールが概ね10km以下の現象を予測するため、メソモデルや局地モデルでは非静力学方程式系を採用しており、これらのモデルでは、鉛直流を質量保存則の式から診断的に計算している。

→ 答えは 誤 です。

非静力学方程式系 とは、積乱雲や積乱雲群のような、鉛直スケールに比べて水平スケールが十分大きいとはいえない現象を予測するための手法で、メソモデル（MSM）や局地モデル（LFM）などで採用されています。

この方程式系には鉛直流の予報方程式があり、鉛直流はその方程式を時間積分することで求めています。

したがって、メソモデル（MSM）や局地モデル（LFM）では「鉛直流は質量保存則の式から診断的に計算している」のではなく、「非静力学方程式系の鉛直流の予報方程式を時間積分して鉛直流を計算しています」ので、答えは 誤 となります。

なお、鉛直流を質量保存則の式から診断的に計算しているのは、全球モデル（GSM）などで採用されている プリミティブ方程式系 です。

プリミティブ方程式系では、鉛直流の予報方程式が静力学平衡の式で置き換わっており、鉛直流の計算にはこの静力学平衡の式は使えません。

しかし、静力学近似の結果として質量保存則の式に時間変化の項が含まれないので、この質量保存則の式を用いて水平風の予測値から診断的に鉛直流を計算しています。

本問の解説：(c)について

（問題）数値予報モデルでは、格子点の物理量で表現した大気の状態を、一定の時間間隔（時間ステップ）で計算を繰り返して将来の大気の状態を予測する。時間ステップを大きくすると計算時間を短縮できるが、ある上限をこえると計算が不安定になり、物理的に意味をなさない値が出力されたり、計算が続けられなくなったりする。

→ 答えは 正 です。

数値予報モデルでは、格子点の物理量で表現した大気の状態を、一定の時間間隔（時間ステップ）で計算を繰り返して将来の大気の状態を予測します。

例えば、全球モデル（GSM）では400秒（６分40秒）、メソモデル（MSM）では20秒、局地モデル（LFM）では８秒ごとに計算を繰り返しています。

しかし、この時間ステップが大きすぎると、計算と計算の間に大気の状態が変化しすぎてしまい、正しい計算ができなくなってしまいます。

これを防ぐためには、時間ステップが、空気の流れの速さ（＝風速など）や、格子点間隔に対して、小さすぎないようにしなければなりません。

この条件のことを CFL条件 （または、クーラン条件）といいます。

（CFLという名前は、この条件を提唱したクーラン、フリードリヒ、ルーウィーの３人の名前の頭文字から取ったものです。）

CFL条件は \( \Delta x \) を格子点間隔、 \( \Delta t \) を時間ステップ、 \( C \) を流れの速さとすると、以下の式で表されます。

\( \displaystyle \frac{\Delta x\;}{\Delta t \;}>C \)

この式は、数値予報モデルで安定した計算を行うためには、 \( \displaystyle\frac{\Delta x \;}{\Delta t \;} \) が \( C \) よりも大きくなければならない、ということを意味しています。

例えば、格子間隔がΔx = 20kmで、風速がC = 50m/sである場合を考えてみます。

Δt を求めるために、CFL条件の「>」を「=」に変えて計算してみると

Δt = Δx / C = 20000[m] / 50[m/s] = 400[s]

となります。

つまり、この場合の時間ステップの上限は400秒となり、これより大きな時間ステップ（500秒や600秒など）では、計算が安定しないということが分かります。

ちなみに、全球モデル（GSM）は2023年３月に格子点間隔が約20kmから約13kmに変更されました。

上記のCFLで計算すると、Δt = Δx / C = 13000[m] / 50[m/s] = 260[s] となり、理論上の時間ステップは約260秒となりますが、現在も格子点間隔が約20kmのときの時間ステップである400秒で計算しています。

また、実際の大気はそのときどきで風速が異なるため、今回のように 50m/s と常に同じというわけではありませんが、その都度、時間ステップは変えませんので、風速が大きいなど最も厳しい気象条件を想定してあてはめることになります。

そのような理由から、ここでは風速を 50m/s にし、厳しい条件を想定して考えています。

したがって、数値予報モデルでは、時間ステップがある上限をこえると計算が不安定になり、物理的に意味をなさない値が出力されたり、計算が続けられなくなったりしますので、答えは 正 となります。

以上より、本問の解答は、(a) 誤 (b) 誤 (c) 正 とする ５ となります。