問7
絶対渦度の保存について述べた次の文章の空欄(a)~(c)に入る数値および語句の組み合わせとして適切なものを、下記の1~5の中から1つ選べ。ただし、渦度はその鉛直成分を指し、緯度φにある空気塊の地球の自転による渦度は 1.46×10-4×sinφ[/s] 、sin30°= 0.5 である。
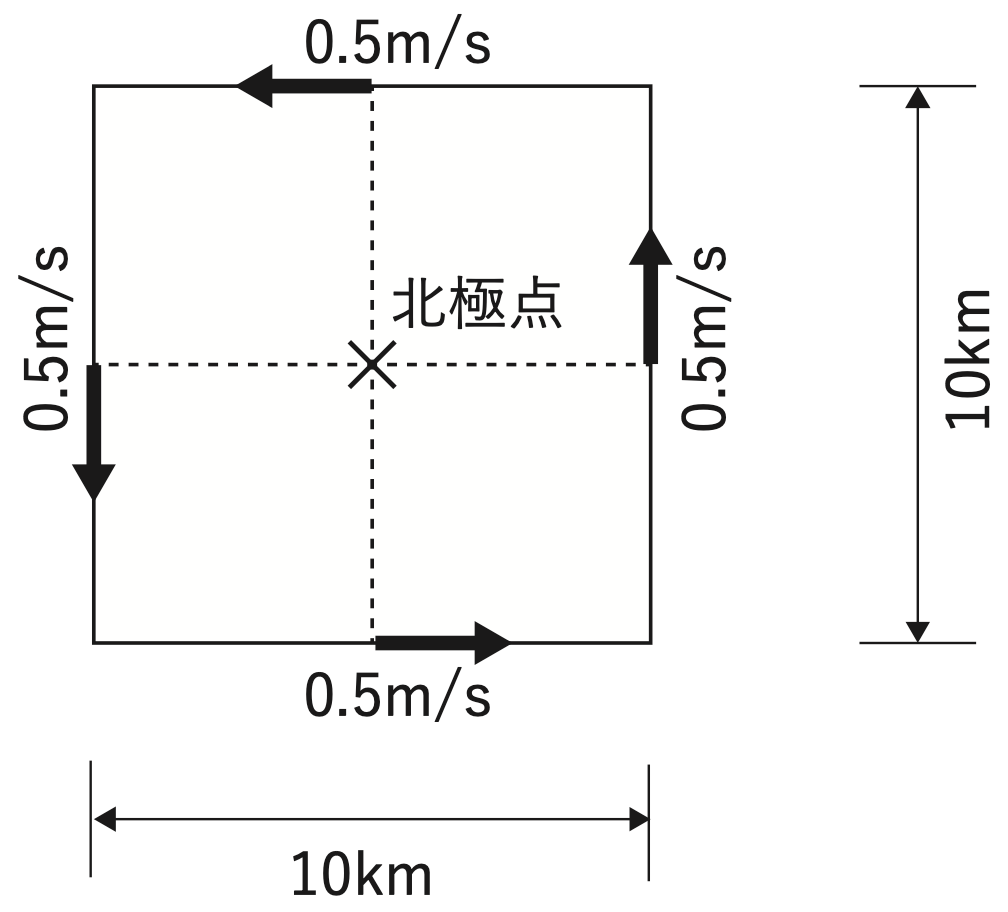
一般に、地球上の空気塊の絶対渦度は、地球の自転による渦度と相対渦度の和で表され、粘性や水平収束・発散がなければ近似的に保存される。北極点にある10km四方の領域内の空気塊を考え、その周りの風の分布が図のように与えられているとする。この領域の中では空気塊の相対渦度が一様とすると、空気塊の相対渦度は (a) である。また、この空気塊が絶対渦度を保存したまま北緯30°まで南下したとき、空気の相対渦度は約 (b) となる。すなわち空気塊の相対渦度は北緯30°に南下すると (c) ことがわかる。
本問は、絶対渦度の保存に関する問題です。
前提知識:渦度について
まずは、渦度について理解しておきましょう。
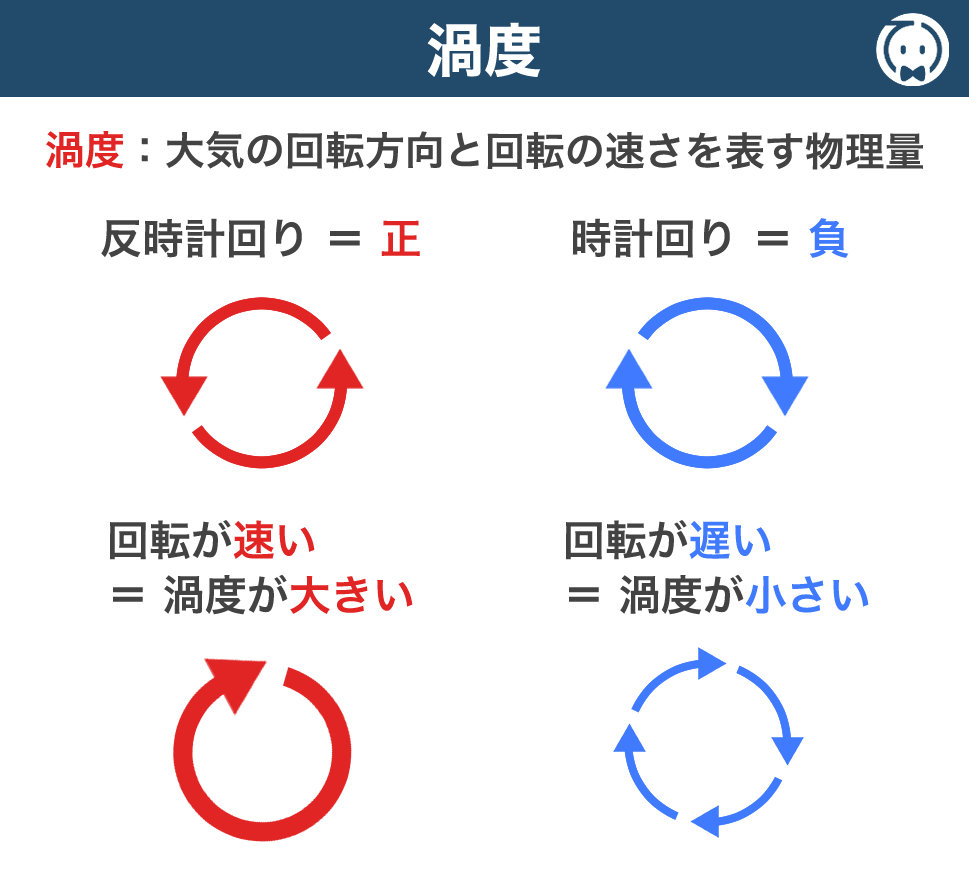
渦度(読:うずど)とは、大気の回転方向と回転の速さを表す物理量です。
大気の流れはまっすぐ進むものだけではなく、回転しているものもあります。
この回転している状態を表すものが渦度です。
また、回転方向には、反時計回り(正)と時計回り(負)があり、
回転が速いほど、渦度が大きいと表現します。
相対渦度 とは、低気圧や高気圧など、風の曲率やシアによって生じる渦度のことです。
相対渦度は下式で表されます。
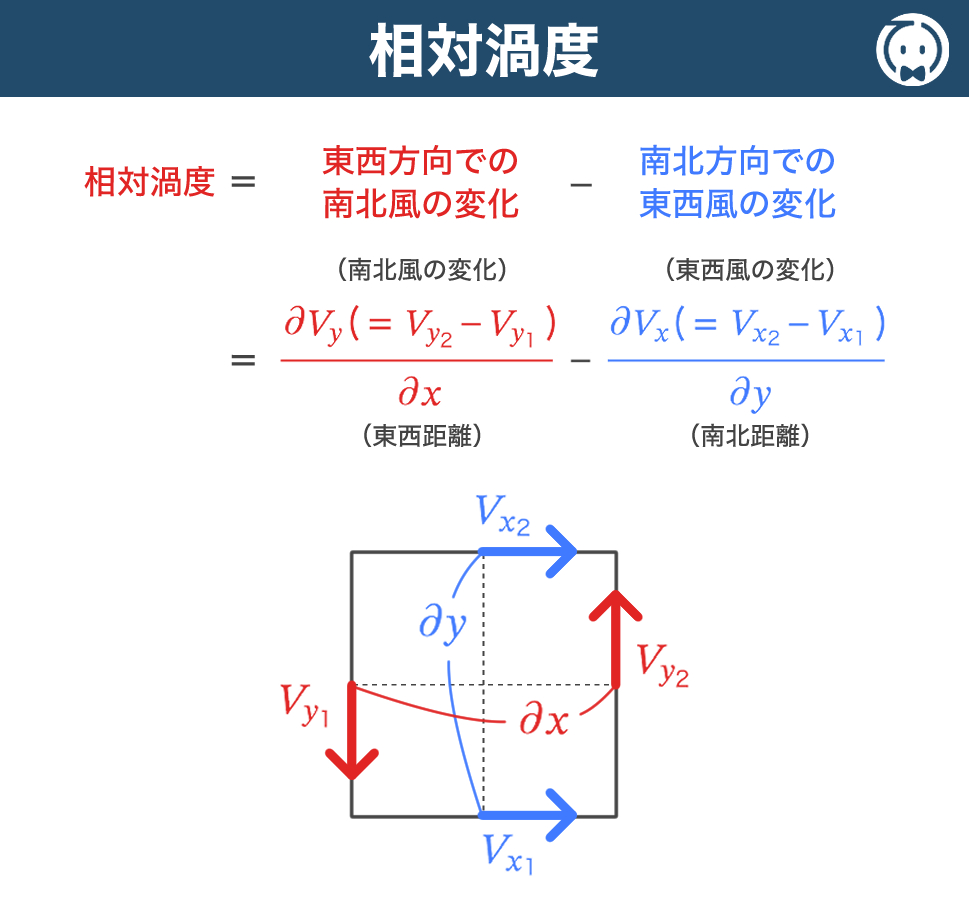
なぜ上式で表されるかは、下記記事を読んでみてください。

惑星渦度 とは、地球の自転によって生じる渦度のことです。
緯度φにある空気塊の惑星渦度は下式で表されます。
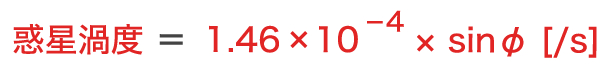
sin90°= 1、sin0°= 0 なので、惑星渦度は、緯度が高いほど大きく、極(北極・南極)では最大、赤道ではゼロとなります。
絶対渦度 とは、相対渦度と惑星渦度の和のことです。
絶対渦度は、大気中に粘性や水平収束・発散がなければ近似的に保存されます。
これを 絶対渦度保存則 といいます。
(絶対渦度保存則は、流体の運動方程式、特に渦度方程式から導かれます。粘性や水平収束・発散がない大気中では、渦度は時間的に変化しない保存量であることが証明されています。また、地球の自転を考慮に入れると、絶対渦度が保存されることが示されますが、細かい証明は気象予報士試験の範囲外なので省略します。)
本問の解説:(a)について
(問題)一般に、地球上の空気塊の絶対渦度は、地球の自転による渦度と相対渦度の和で表され、粘性や水平収束・発散がなければ近似的に保存される。北極点にある10km四方の領域内の空気塊を考え、その周りの風の分布が図のように与えられているとする。この領域の中では空気塊の相対渦度が一様とすると、空気塊の相対渦度は (a) である。

→ 答えは 2.0×10-4 /s です。
相対渦度は下式で求めることができます。(北向き、東向きが正)
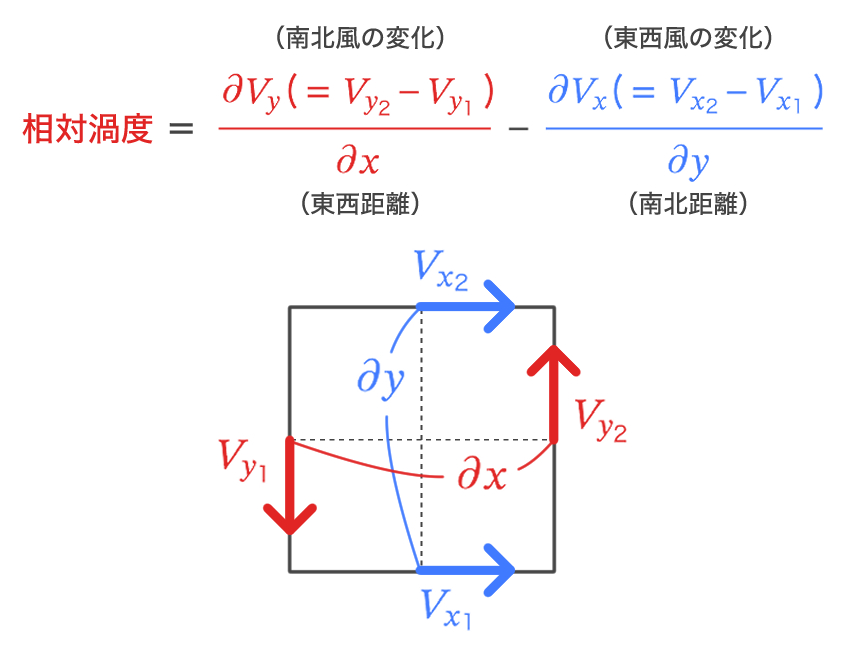
この式に、問題の数値を代入すると
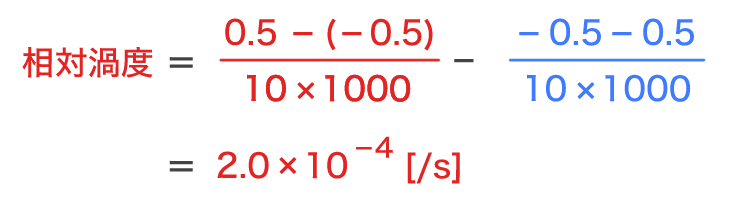
となりますので、答えは 2.0×10-4 /s となります。
本問の解説:(b)について
(問題)この空気塊が絶対渦度を保存したまま北緯30°まで南下したとき、空気の相対渦度は約 (b) となる。(ただし、渦度はその鉛直成分を指し、緯度φにある空気塊の地球の自転による渦度は 1.46×10-4×sinφ[/s] 、sin30°= 0.5 である。)
→ 答えは 2.7×10-4/s です。
絶対渦度とは、惑星渦度(地球の自転による渦度)と相対渦度の和であり、問題文より、緯度φにある空気塊の地球の自転による渦度は 1.46×10-4×sinφ[/s] と与えられています。
本問で考えている空気塊は北極点にありますので、北極点(=緯度90°)での絶対渦度は、

となります。(sin90°= 1)
一方、空気塊が北緯30°まで南下した時の絶対渦度は、相対渦度を ζ30 とすると、

となります。(sin30°= 0.5)
これらが等しいので、求める ζ30 は

となります。
したがって、答えは 2.7×10-4/s となります。
本問の解説:(c)について
(問題)すなわち空気塊の相対渦度は北緯30°に南下すると (c) ことがわかる。
→ 答えは 強まる です。
問題 (a) より、北緯90°( =北極点 ) での相対渦度は 2.0×10-4 /s であり、
問題 (b) より、北緯30°での相対渦度は 2.7×10-4 /s であることが分かりました。
したがって、空気塊の相対渦度は北緯30°に南下すると強まりますので、答えは 強まる となります。
以上より、本問の解答は、(a) 2.0×10-4/s (b) 2.7×10-4/s (c) 強まる とする 4 となります。
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、執筆者「terurunnikki@gmail.com」までご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。



コメント