問12
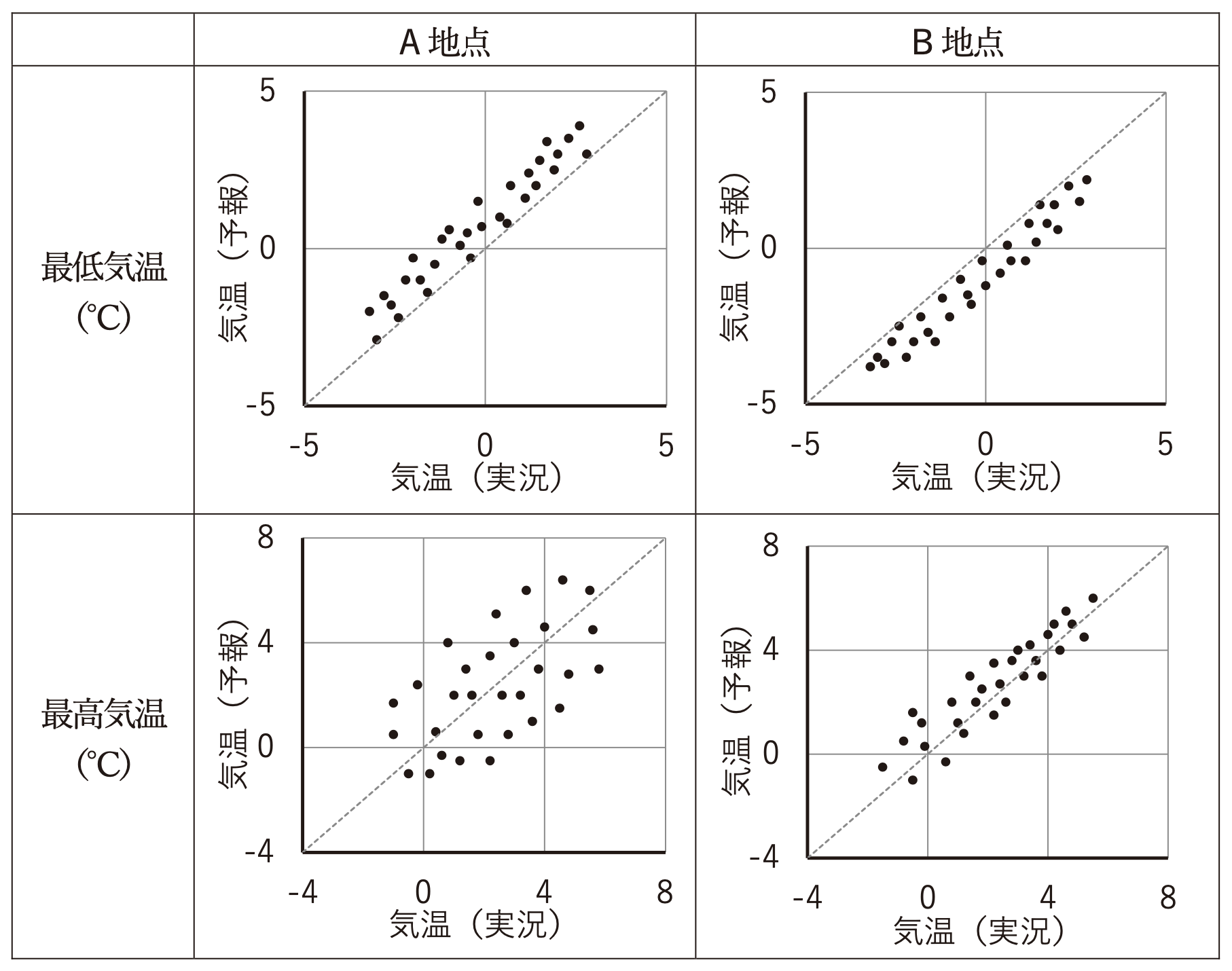
図はA地点、B地点における、冬季の日々の最高気温と最低気温について、30日間の実況と予報の分布を示したものである。この図について述べた次の文 (a) ~ (c) の正誤の組み合わせとして正しいものを、下記の1~5の中から1つ選べ。ただし、見逃し率および空振り率は全予報数に対する割合とする。
(a) 最低気温の予報の平均誤差 (ME) に正の偏りがあるのはA地点であり、最高気温の予報の二乗平均平方根誤差 (RMSE) を比較して予報精度が良いのはB地点である。
(b) 冬日の予報の見逃し率は、A地点の方がB地点よりも低い。
(c) 真冬日の予報の空振り率は、A地点の方がB地点よりも低い。
本問は、気温予報の検証に関する問題です。
問題を解く前に、用語の整理をしておきましょう。
平均誤差
平均誤差(ME:Mean Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の系統的な偏りを評価する指標です。
平均誤差は下式で定義され、予報値から実況値を差し引いた予報誤差の合計を、予報回数で割って求めます。
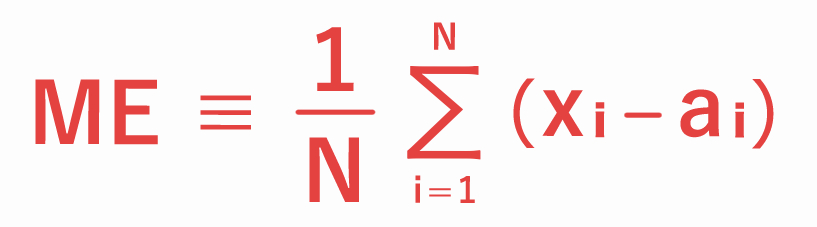
(N:全事例数、xi:予報値、ai:実況値)
平均誤差は、値がプラスであれば予報が過大、マイナスであれば予報が過小であることを意味します。
つまり、値が0のときは、平均的に見て、予報が正にも負にも偏っていないということです。
しかし、正の誤差と負の誤差が打ち消し合う場合にも、値は小さくなりますので、値が小さいほど予報精度が良いわけではありません。
 てるらん
てるらん平均誤差は、実況値に比べて、予報値が全体的に大きいのか、小さいのかを判別する指標なんだね!
二乗平均平方根誤差
二乗平均平方根誤差(RMSE:Root Mean Square Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の大きさを評価する指標です。
二乗平均平方根誤差は下式で定義され、予報値と実況値の誤差を二乗して平均し、その平方根を取って求めます。
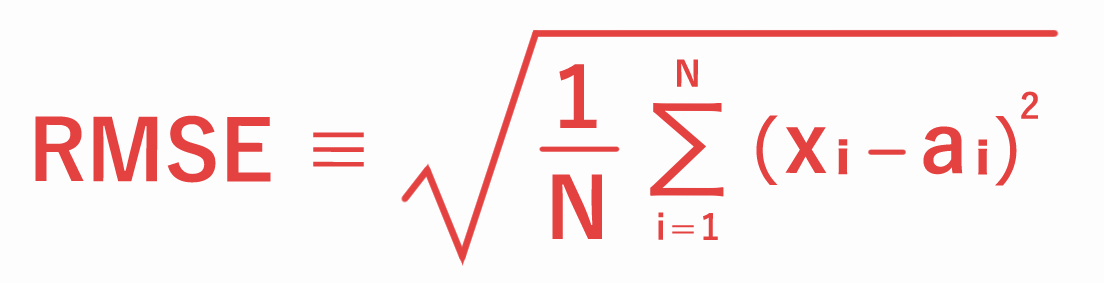
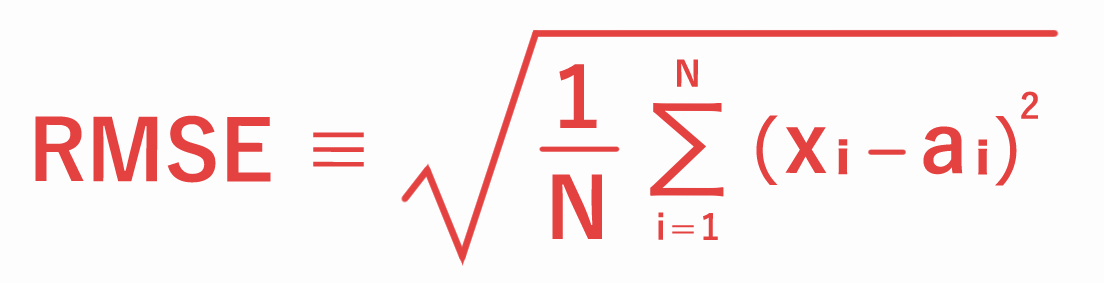
(N:全事例数、xi:予報値、ai:実況値)
二乗平均平方根誤差は、誤差を二乗していますので、誤差の正負(系統的な偏り)ではなく、誤差の大きさを評価します。
つまり、値が0に近いほど予報精度が良く、値が大きいほど誤差が大きいということです。



平均誤差は、予報誤差の偏りを評価していたのに対して、
二乗平均平方根誤差は、予報誤差の大きさを評価しているんだよ!
見逃し率
見逃し率 とは、現象なしと予想したのに、現象が起きた日の割合のことです。
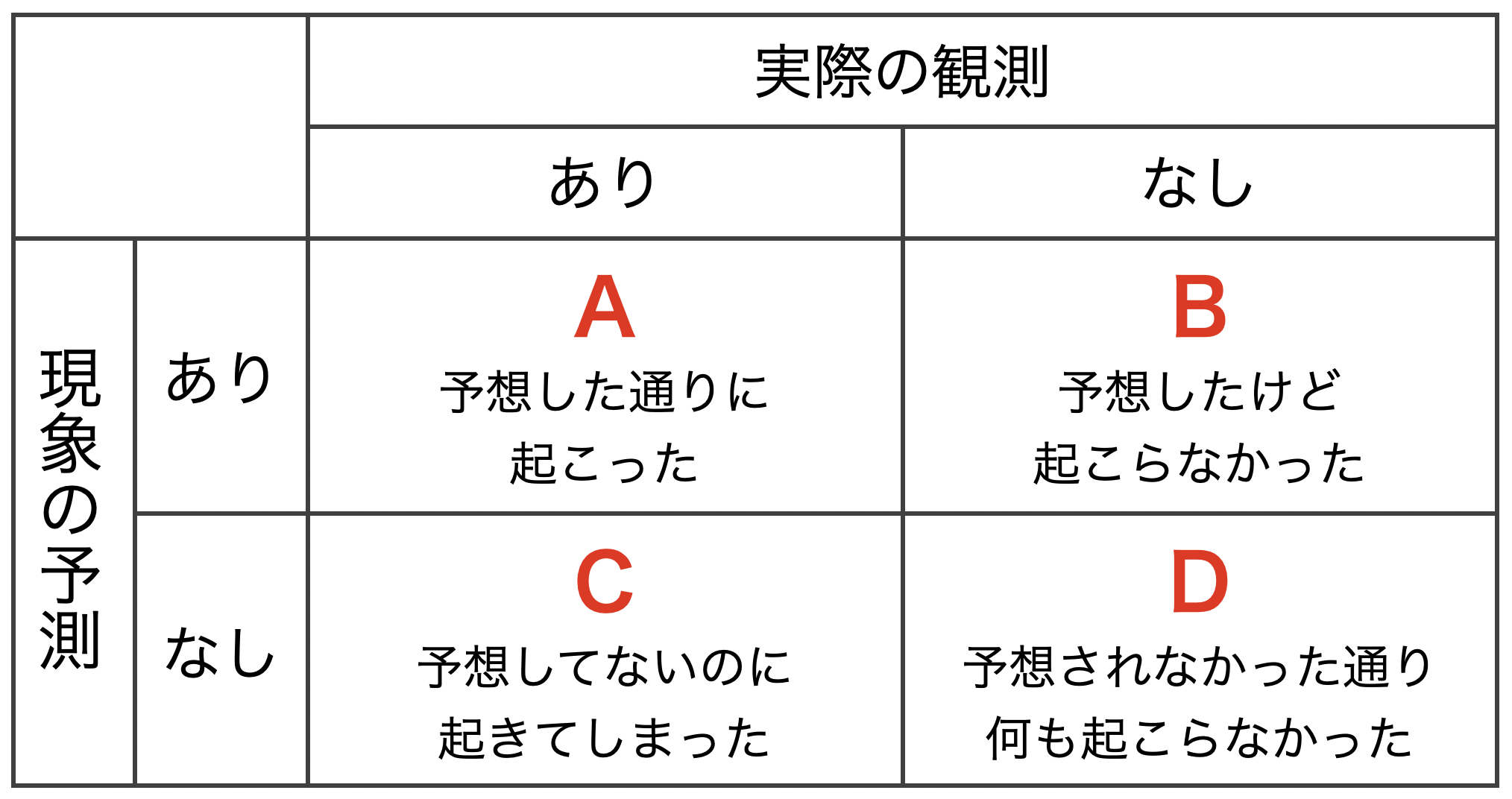

見逃し率 = C / N
(N:全事例数(=A+B+C+D)、C:見逃し数)



野球のバッターが、ボール球だと思って見逃したのにストライクだった!
みたいなかんじだね!
空振り率
空振り率 とは、現象ありと予想したのに、現象が起きなかった日の割合のことです。


空振り率 = B / N
(N:全事例数(=A+B+C+D)、B:空振り数)



野球のバッターが、ストライクだと思ってバットを振ったのに、実際はボール球だった!
みたいなかんじだよ!
本問の解説:(a) について
(問題)最低気温の予報の平均誤差 (ME) に正の偏りがあるのはA地点であり、最高気温の予報の二乗平均平方根誤差 (RMSE) を比較して予報精度が良いのはB地点である。
→ 答えは 正 です。
平均誤差(ME)は(予報値−実況値)の平均です。
平均誤差は、値がプラスであれば、予報が過大、マイナスであれば、予報が過小であることを意味します。
問題の図をみると、A地点の最高気温は、常に実況値より予報値の方が高いため、予報が正に偏っていることが分かります。
一方、B地点の最高気温は、常に実況値より予報値の方が低いため、予報が負に偏っていることが分かります。
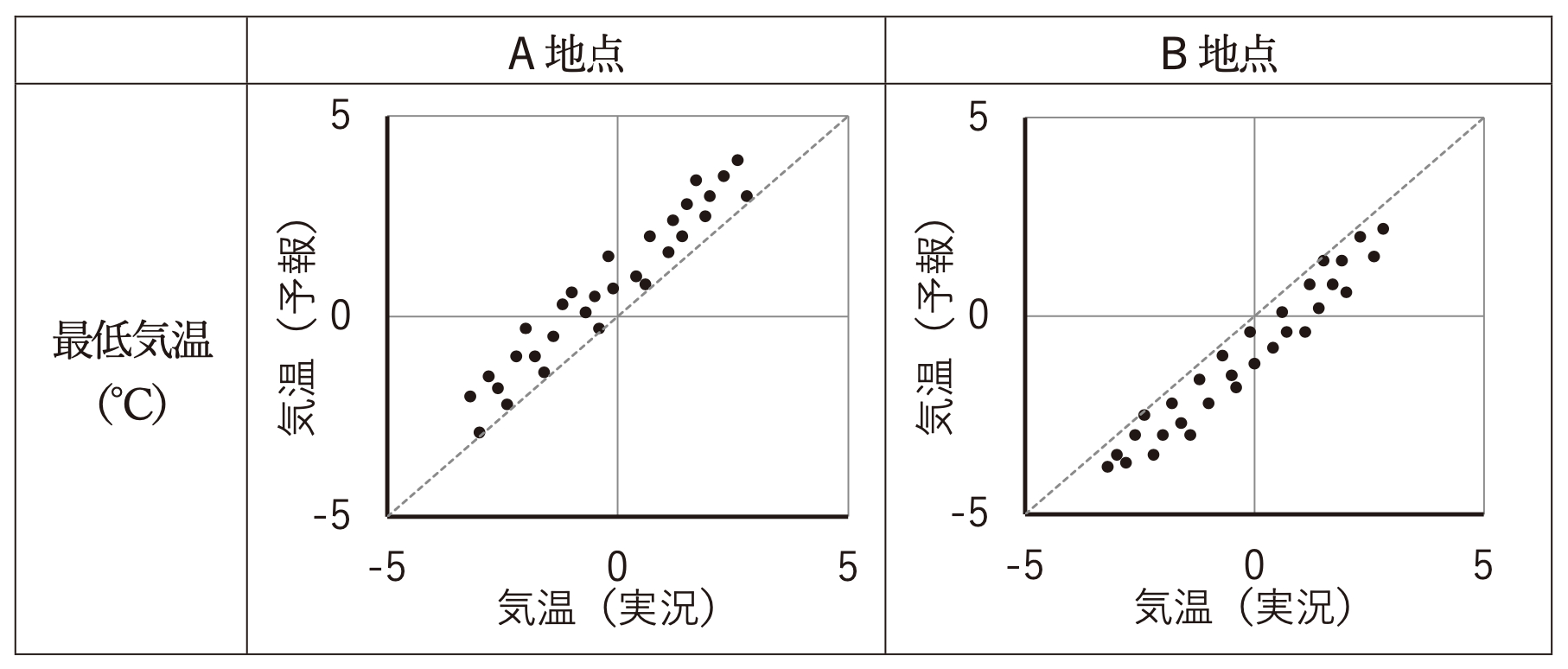

また、二乗平均平方根誤差(RMSE)は、(予報値−実況値)の二乗平均を平方根したものです。
この値が小さいほど、予報の精度が良いということができます。
問題の図を見ると、B地点の方が、A地点よりも予報のバラつきが小さく、RMSEも小さくなるため、予報精度が良いことが分かります。
したがって、最低気温の予報の平均誤差 (ME) に正の偏りがあるのはA地点であり、最高気温の予報の二乗平均平方根誤差 (RMSE) を比較して予報精度が良いのはB地点ですので、答えは 正 となります。
本問の解説:(b) について
(問題)冬日の予報の見逃し率は、A地点の方がB地点よりも低い。(ただし、見逃し率は全予報数に対する割合とする。)
→ 答えは 誤 です。
冬日 とは、日最低気温が0℃未満の日のことです。
冬日の予報の見逃し率 とは、最低気温が0℃以上(=冬日でない)と予想したのに、実況が0℃未満であった(=冬日だった)日の割合のことです。
つまり、下図の赤枠の部分が、冬日の予報の見逃しです。
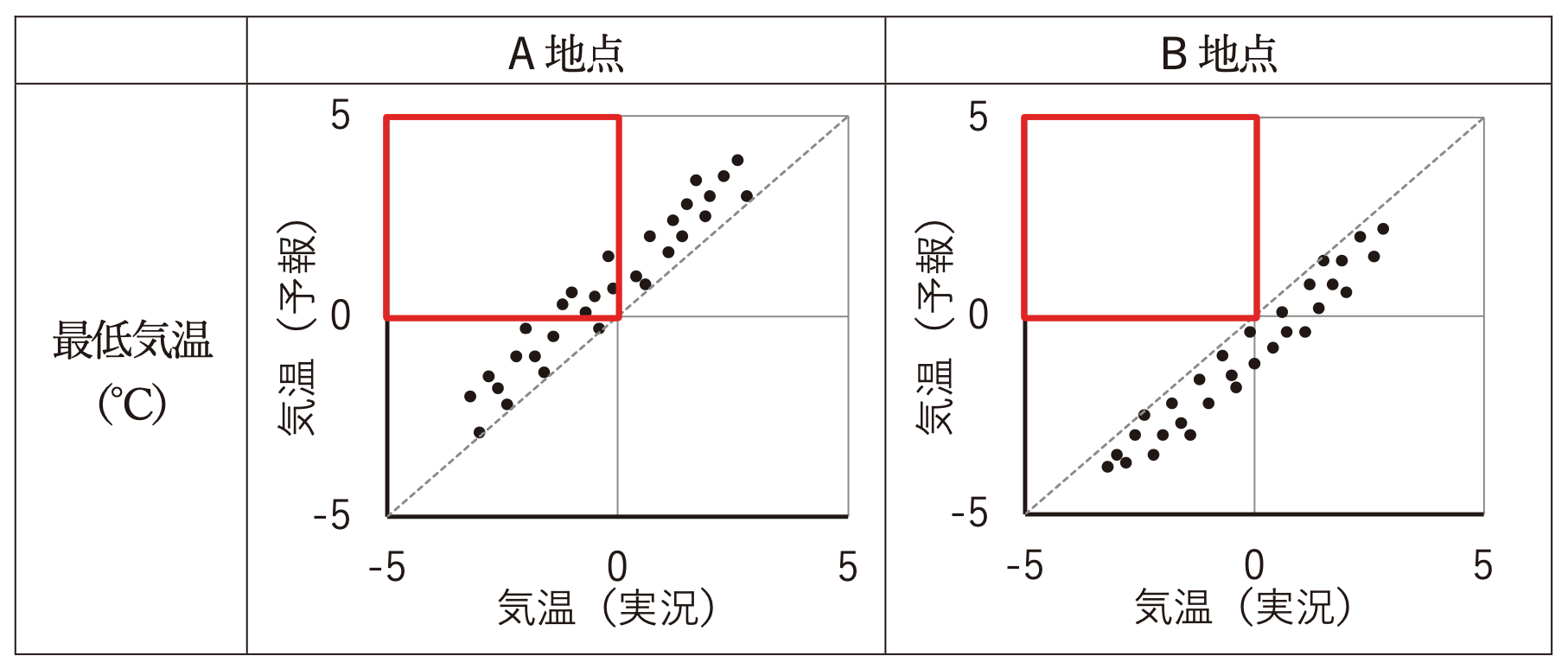

実際に計算してみると
A地点の冬日の予報の見逃し率 = 6/30 = 0.2
B地点の冬日の予報の見逃し率 = 0/30 = 0
となり、冬日の予報の見逃し率は、A地点の方がB地点よりも高いことが分かります。
したがって、冬日の予報の見逃し率は、A地点の方がB地点よりも「低い」ではなく「高い」ので、答えは 誤 となります。
本問の解説:(c) について
(問題)真冬日の予報の空振り率は、A地点の方がB地点よりも低い。(ただし、空振り率は全予報数に対する割合とする。)
→ 答えは 誤 です。
真冬日 とは、日最高気温が0℃未満の日のことです。
真冬日の予報の空振り率 とは、最高気温が0℃未満(=真冬日)と予想したのに、実況が0℃以上であった(=真冬日でなかった)日の割合のことです。
つまり、下図の赤枠の部分が、真冬日の予報の空振りです。
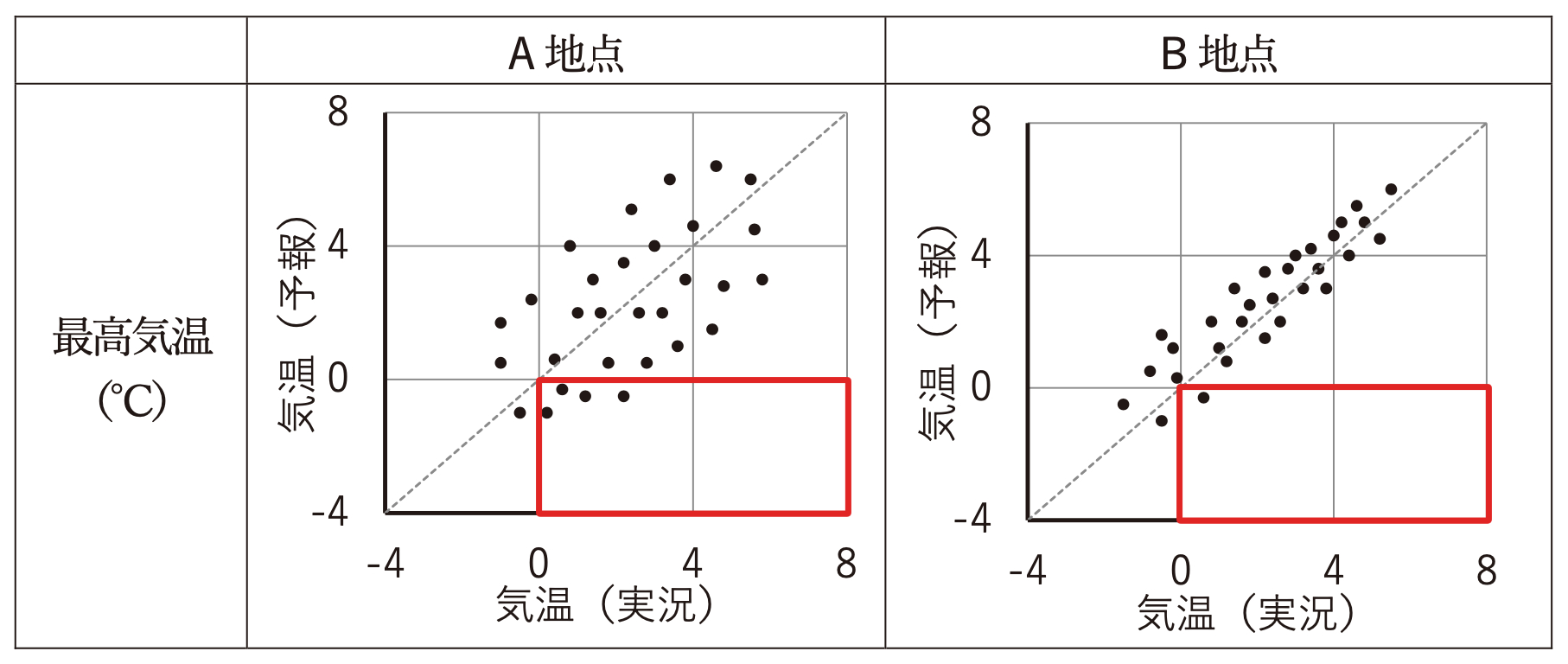

実際に計算してみると
A地点の真冬日の予報の空振り率 = 4/30 = 0.13
B地点の真冬日の予報の空振り率 = 1/30 = 0.03
となり、真冬日の予報の空振り率は、A地点の方がB地点よりも高いことが分かります。
したがって、真冬日の予報の空振り率は、A地点の方がB地点よりも「低い」ではなく「高い」ので、答えは 誤 となります。
以上より、本問の解答は、(a) 正 (b) 誤 (c) 誤 とする 3 となります。
書いてある場所:ー
書いてある場所:ー
書いてある場所:P304〜320(予報精度評価)
書いてある場所:P452〜463(予報精度の評価)
書いてある場所:P186〜192(予報精度評価の種類)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。








コメント