問3
地点 \( \text{A}\)、\( \text{B}\)、\( \text{C}\) における地上(高度0m)から高度1000mまでの気層の気温の平均値がそれぞれ \( T_\text{A}\)、\( T_\text{B}\)、\( T_\text{C}\) 、混合比がそれぞれ \(q_\text{A}\)、\( q_\text{B}\)、\( q_\text{C}\) であり、また、\( T_\text{A}<T_\text{B}=T_\text{C} \) かつ \( q_\text{A}=q_\text{B}<q_\text{C} \) となっている。各地点の地上気圧が等しいとき、地点 \( \text{A} \)、\( \text{B} \)、\( \text{C} \) における高度1000mの気圧 \( P_\text{A} \)、\( P_\text{B} \)、\( P_\text{C} \) の大小関係として正しいものを下記の1〜5の中から1つ選べ。ただし、いずれの地点でも大気は静力学平衡の状態にあり、重力加速度は一定とする。
混合比(予備知識)
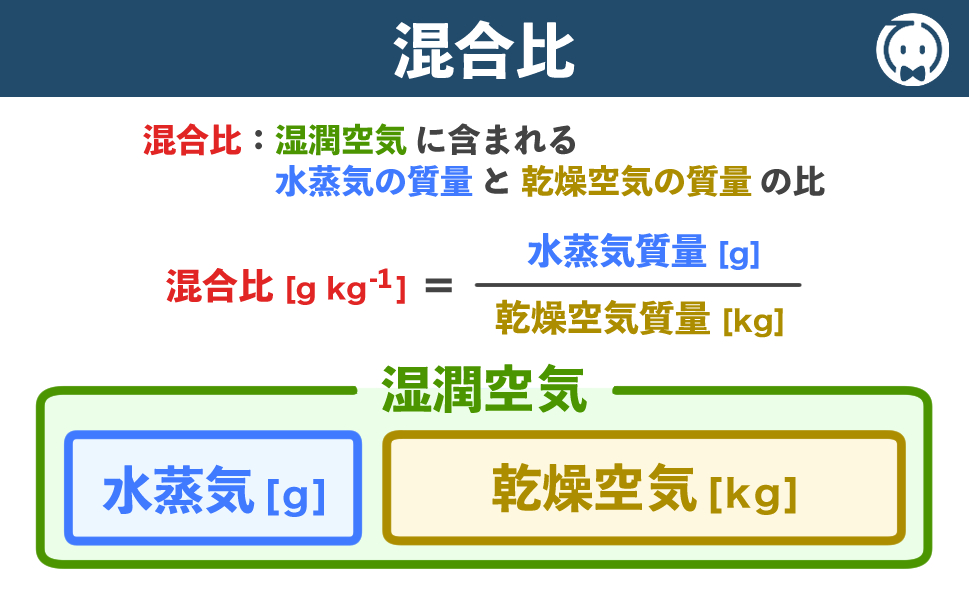
混合比(読:こんごうひ)とは湿潤空気に含まれる「水蒸気の質量」と「乾燥空気の質量」の比のことです。
 てるるん
てるるん簡単に言うと、水蒸気を含んでいる湿った空気の中で、乾燥空気と水蒸気が何:何の割合で存在しているかを表したものだよ!
式で書くとこうなります。
\(\text{混合比}=\displaystyle\frac{\text{水蒸気質量 [g]}}{\text{乾燥空気質量 [㎏]}}\)
乾燥空気は湿潤空気より重い(予備知識)
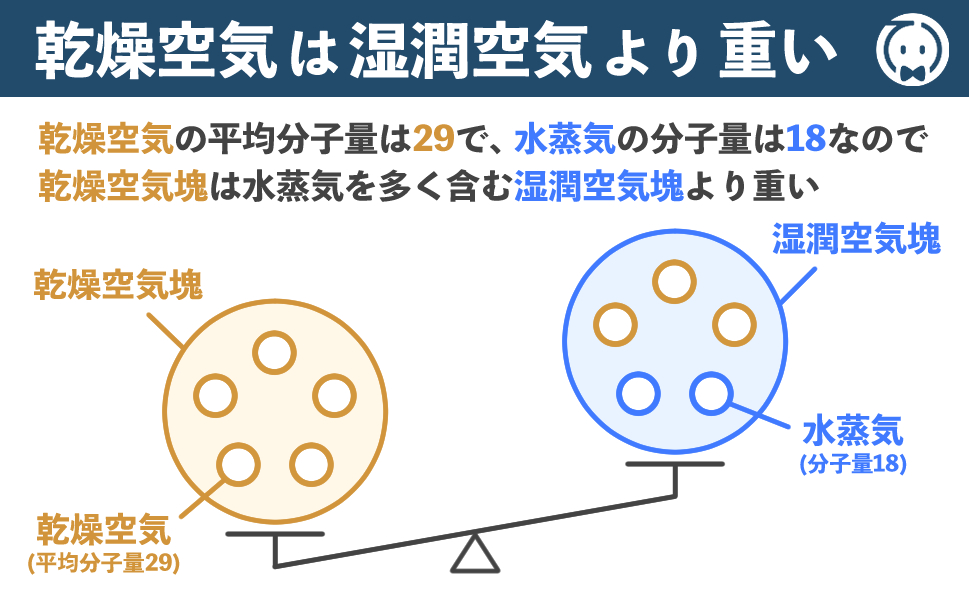

乾燥空気は湿潤空気より重い



上の図を見ながら一緒に考えてみよう!
乾燥空気は約78%が窒素N2(分子量28)で、約21%が酸素O2(分子量32)です。
ですので、乾燥空気の平均分子量は29(28 × 0.78 + 32 × 0.22)となります。
一方、水蒸気はH2Oなので分子量は18です。
アボガドロの法則(=すべての気体は同温・同圧のとき、同体積中に同数の分子を含んでいるという法則)より、乾燥空気塊であっても、湿潤空気塊であっても、同温・同圧・同体積の空気には、同じ数の分子が含まれます。
ここでは簡単のため、同温・同圧・同体積の空気塊に5個の分子が含まれているとしましょう。
このとき、乾燥空気塊の分子量は145(29 × 5)で、湿潤空気塊の分子量は123(29 × 3 + 18 × 2)なので、乾燥空気塊は湿潤空気塊より重くなります。
本問の解説:\( P_\text{A} \) と \( P_\text{B} \) の大小関係について
(問題)地点 \( \text{A}\)、\( \text{B}\) における地上(高度0m)から高度1000mまでの気層の気温の平均値がそれぞれ \( T_\text{A}\)、\( T_\text{B}\)、混合比がそれぞれ \(q_\text{A}\)、\( q_\text{B}\) であり、また、\( T_\text{A}<T_\text{B} \) かつ \( q_\text{A}=q_\text{B} \) となっている。各地点の地上気圧が等しいとき、地点 \( \text{A} \)、\( \text{B} \) における高度1000mの気圧 \( P_\text{A} \)、\( P_\text{B} \) の大小関係を求めよ。
→ 答えは \( P_\text{A} < P_\text{B} \) です。


気温差(\( T_\text{A} < T_\text{B} \))は、空気の膨らみによる気圧差を生じます。
混合比は同じ(\( q_\text{A} = q_\text{B} \))なので、空気分子の重さによる気圧差は生じません。
上図の例では、Aの混合比は \( \frac{4}{6} = \frac{2}{3} \) で、Bの混合比は \( \frac{2}{3} \) なので、混合比は同じです。
ですので、地点 \( \text{A} \) 、\( \text{B} \) 間では、空気の膨らみによる気圧の大小関係を求めます。



空気は暖められると膨張して軽くなるから、気圧は低くなるよ!
逆に、冷えると圧縮して重くなるから、気圧は高くなるよ!
したがって、\( T_\text{A} < T_\text{B} \) より、地点 \( \text{B} \) の空気の方が膨張して軽くなっているので、\( P_\text{A} < P_\text{B} \) となります。
本問の解説:\( P_\text{B} \) と \( P_\text{C} \) の大小関係について
(問題)地点 \( \text{B}\)、\( \text{C}\) における地上(高度0m)から高度1000mまでの気層の気温の平均値がそれぞれ \( T_\text{B}\)、\( T_\text{C}\)、混合比がそれぞれ \(q_\text{B}\)、\( q_\text{C}\) であり、また、\( T_\text{B}=T_\text{C} \) かつ \( q_\text{B}<q_\text{C} \) となっている。各地点の地上気圧が等しいとき、地点 \( \text{B} \)、\( \text{C} \) における高度1000mの気圧 \( P_\text{B} \)、\( P_\text{C} \) の大小関係を求めよ。
→ 答えは \( P_\text{B} < P_\text{C} \) です。
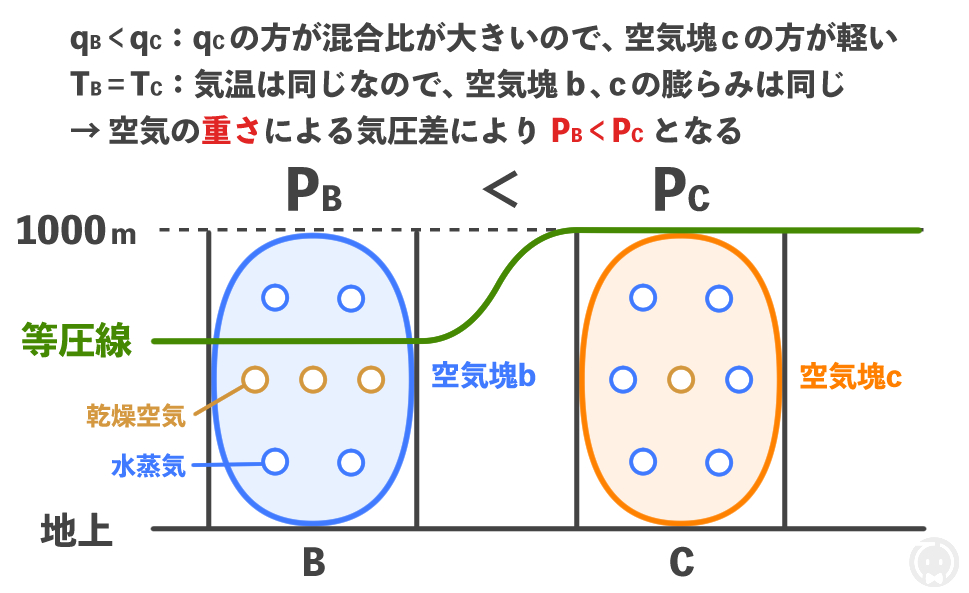

気温は同じ(\( T_\text{B} = T_\text{C} \))なので、空気の膨らみによる気圧差は生じません。
混合比差(\( q_\text{B} < q_\text{C} \))は、空気分子の重さによる気圧差を生じます。
ですので、地点 \( \text{B} \) 、\( \text{C} \) 間では、空気分子の重さによる気圧の大小関係を求めます。



混合比が大きいということは、水蒸気を多く含んでいるということだから、空気は軽くなるよ!
逆に、混合比が小さいと、乾燥空気の方が多くなるから、空気は重くなるよ!
上図の例では、空気塊bの混合比 \( q_\text{B} \) は \( \frac{4}{3} \) で、空気塊cの混合比 \( q_\text{C} \) は \( \frac{6}{1} \) なので、空気塊cの混合比 \( q_\text{C} \) の方が大きく、空気塊bより軽いです。
次に、計算を簡単にするため、乾燥空気の分子量を2、水蒸気の分子量を1として考えてみましょう。
すると、地上〜分子量8の位置(地点Bは 1 × 2 + 2 × 3 = 8、地点Cは 1 × 6 + 2 × 1 = 8)で等圧線を引くと、地点 \( \text{C} \) の方が等圧線の高度が高くなります。
言い換えると、空気塊cの方が軽いので、同じ高度でみた時に気圧が高くなります。
したがって、\( q_\text{B} < q_\text{C} \) より、地点 \( \text{C} \) の空気の方が軽いので、\( P_\text{B} < P_\text{C} \) となります。
以上より、\( P_\text{A} < P_\text{B} \) かつ \( P_\text{B} < P_\text{C} \) であるため、答えは \( P_\text{A} < P_\text{B} < P_\text{C} \) となります。



質問をもらったので追加で解説したよ!
下のリンクから補足の解説を見てみてね!
気柱の重さが一番軽い\( P_\text{C} \)が、気圧が1000mで一番高いというところが、理解できません。
気圧は空気の重さと考えていますが、混乱します。
↓回答はこちらをチェック↓
書いてある場所:P61(混合比)
書いてある場所:P48〜49(混合比)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。






コメント
コメント一覧 (2件)
私は資格勉強中の者です。
分からないところがあったので失礼します。
私は、BとCの比較の時に、
混合比qBよりqCの方が大きいため、空気塊Cの方が密度が小さくなり、気圧の比較も、PC<PBだと考えました。
本当に同じ高度で比べると、気圧が高くなるのは、密度の小さいCの空気塊なのでしょうか?P=ρRTとは別の考え方があるのでしょうか?
恐れいりますが、教えて頂けると幸いです。
はる様
コメントありがとうございます。
本問では、高度1000mでの気圧PA、PB、PCの大小関係を求めます。
また、地上(高度0m)から高度1000mまでの混合比はqC>qBなので、
地上(高度0m)から高度1000mまでの空気の密度は
(空気塊Cの密度)<(空気塊Bの密度)となります。
密度が小さいということは、空気が軽いということですので、
地上(高度0m)から高度1000mまでの空気の重さは
(空気塊Cの重さ)<(空気塊Bの重さ)となります。
気圧=空気の重さなので、単純に考えると
気圧もPC<PBとなりそうですよね。
しかし、地上気圧が同じという点に着目します。
地上気圧が同じということは、地上からはるか上空(例えば、高度数十kmくらい)までの
空気の重さが同じということです。
先ほど求めたように(空気塊Cの重さ)<(空気塊Bの重さ)ですので
地上(高度0m)から高度1000mまでの気圧をそれぞれPC’、PB’とすると、
PC’<PB’となります。
仮に、地上気圧を1000hPa、PC’=50hPa、PB’=100hPaとして考えてみましょう。
PB、PCは、高度1000mでの気圧(つまり、高度1000mからはるか上空までの空気の重さ)ですので、
PB=地上気圧 – PB’
=1000hPa – 100hPa
=900hPa
PC=地上気圧 – PC’
=1000hPa – 50hPa
=950hPa
となり、PB < PC となります。