【第62回】2024年８月試験（学科専門試験）問５（数値予報の誤差とアンサンブル予報）

本問は、数値予報の誤差とアンサンブル予報に関する問題です。

本問の解説：(a) について

（問題）数値予報には、数値予報モデルやその初期値が完全でないことなどに起因する誤差が含まれる。地球大気を扱う数値予報モデルでは、格子間隔より小さなスケールの現象によって生じる効果を、(a)格子点における物理量を用いて近似的に評価している ので、実際の現象とは厳密に一致せず、誤差が生じる要因の一つとなっている。

→ 答えは 正 です。

まず、数値予報 とは、計算機（コンピューター）を用いて、地球大気や海洋・陸地の状態の変化を数値シミュレーションによって予測することをいいます。

具体的には、最初に地球大気や海洋・陸地を細かい格子に分割し、世界から送られてくる観測データに基づいて、それぞれの格子に、ある時刻の気温・風などの気象要素や海面水温・地表面温度などの値を割り当てます。

例えば、全球モデル（GSM）は約 13 km、メソモデル（MSM）は約５kmの格子間隔で分割し、計算を行います。

（全球モデル（GSM）の格子間隔は、令和５年３月に約20kmから約13kmに改良され、より細かな現象まで予測できるようになりました。）

次に、こうして求めた「今」の状態から、物理学や化学の法則に基づいてそれぞれの値の時間変化を計算することで「将来」の状態を予測します。

この計算に用いるコンピュータープログラムを 数値予報モデル と呼んでいます。

しかし、数値予報では、格子点間隔の５〜８倍以上のスケールの現象でなければ表現できないと言われています。

例えば、全球モデル（GSM）の格子点間隔は約 13 kmですので、最低でも約 65 km以上の水平スケールの現象でないと表現できないということです。

しかし、小さいスケールの現象が大きいスケールの現象に影響を及ぼすこともありますので、数値予報モデルで直接表現できないからといって、その影響を無視することはできません。

このため、数値予報モデルでは、格子間隔より小さなスケールの現象によって生じる効果を、格子点における物理量を用いて近似的に評価する必要があります。

その計算方法を パラメタリゼーション といいます。

したがって、数値予報モデルでは、格子間隔より小さなスケールの現象によって生じる効果を、格子点における物理量を用いて近似的に評価していますので、答えは 正 となります。

本問の解説：(b) について

（問題）(b)仮に数値予報モデルが完全であり、初期値に含まれる誤差が微小であったとしても、大気の持つカオス的な性質により、予報時間が長くなるにしたがって予報誤差は急速に増大することが知られている。

→ 答えは 正 です。

数値予報モデルには、連続的な気象現象を離散的な格子点で表現する際の誤差や、物理過程のパラメタリゼーションによる誤差があります。

仮に、これらの誤差がない理想的なモデルを用いたとしても、初期値に誤差が含まれていた場合、予報時間が長くなるほど、大気の持つカオス的な性質により、誤差が急速に増大してしまいます。

例えば、メソスケール現象（積雲対流など）のように時空間スケールが小さく、非線形性が卓越する現象では、初期値に含まれる誤差が短時間のうちに増大し、予報の決定論的限界（＝予測可能な時間の限界）に達してしまいます。

したがって、仮に数値予報モデルが完全であり、初期値に含まれる誤差が微小であったとしても、大気の持つカオス的な性質により、予報時間が長くなるにしたがって予報誤差は急速に増大しますので、答えは 正 となります。

本問の解説：(c) について

（問題）数値予報の誤差を予め把握するため、気象庁のメソアンサンブル予報では、(c)初期値と側面境界値に少しずつ異なった誤差 (摂動) を加えた複数の予測を行っており 、さらに 2023年３月からは、数値予報モデルの物理過程の不確実性を考慮するために、モデルアンサンブル手法の一つである確率的物理過程強制法が導入されている。

→ 答えは 正 です。

アンサンブル予報 とは、数値予報モデルに初期値の小さな揺らぎ（摂動）を与えて複数の予測を行い、その集団（アンサンブル）から未来の大気の状態を確率的に予測する手法のことです。

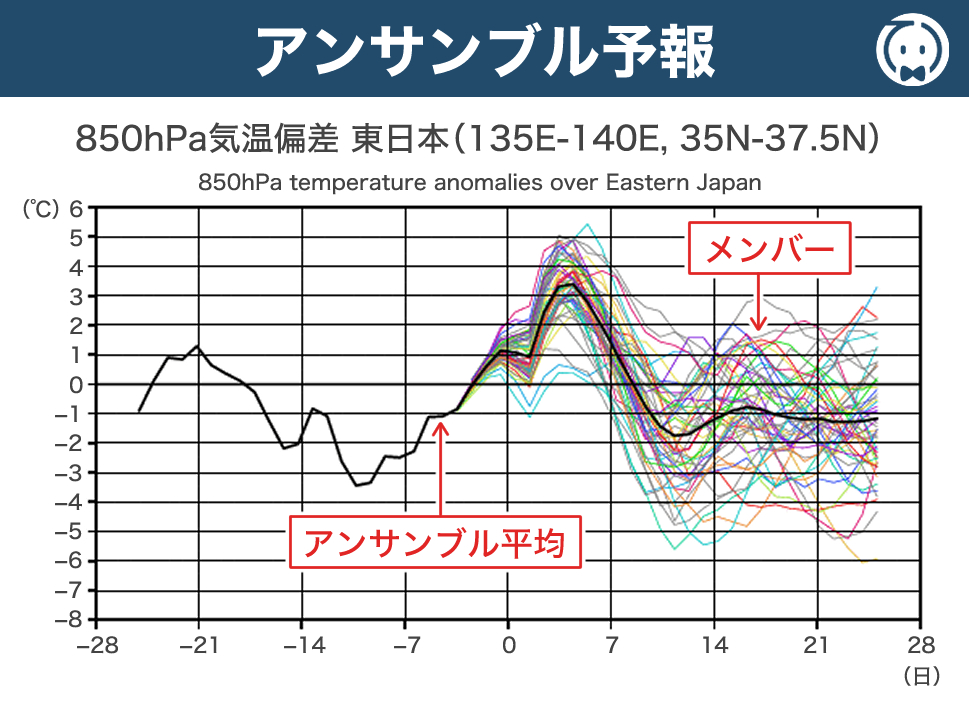
このとき、それぞれの数値予報モデルの予測をアンサンブルメンバー（または単にメンバー）、摂動を加えていないアンサンブルメンバーをコントロールラン、全メンバーを平均したものをアンサンブル平均といいます。

アンサンブル予報は、大気の持つカオス的な性質による予報誤差の急速な増大への対策として行われるもので、初期値や物理過程などの不確実性を考慮して多数の数値予報を行います。

その結果から各メンバーの平均やばらつきの程度などの統計的な情報が得られるので、予測値の信頼度を評価することや、気象現象の発生を確率的に予測することが可能になります。

気象庁の全球アンサンブル予報では、初期値と物理過程に少しずつ異なった誤差（摂動）を加えた複数の予測を行っていますが、メソアンサンブル予報ではそれらに加えて側面境界値にも摂動を加えています。

また、問題文にある 確率的物理過程強制法（SPPT法：Stochastically Perturbed Parametrization Tendencies scheme）とは、数値予報モデルの物理過程のパラメタリゼーションが持つ不確実性を取り扱う手法の一つです。

この手法では、数値予報の各時間ステップにおいて、パラメタリゼーションによって計算される気温・比湿・風の時間変化量に、時間・空間相関が考慮された小さな乱数をかけたものを摂動とみなし、これをパラメタリゼーションによる変化量に加えてアンサンブル予報を行います。

この手法は、全球アンサンブル予報では2010年12月から、メソアンサンブル予報では2023年３月から導入されています。

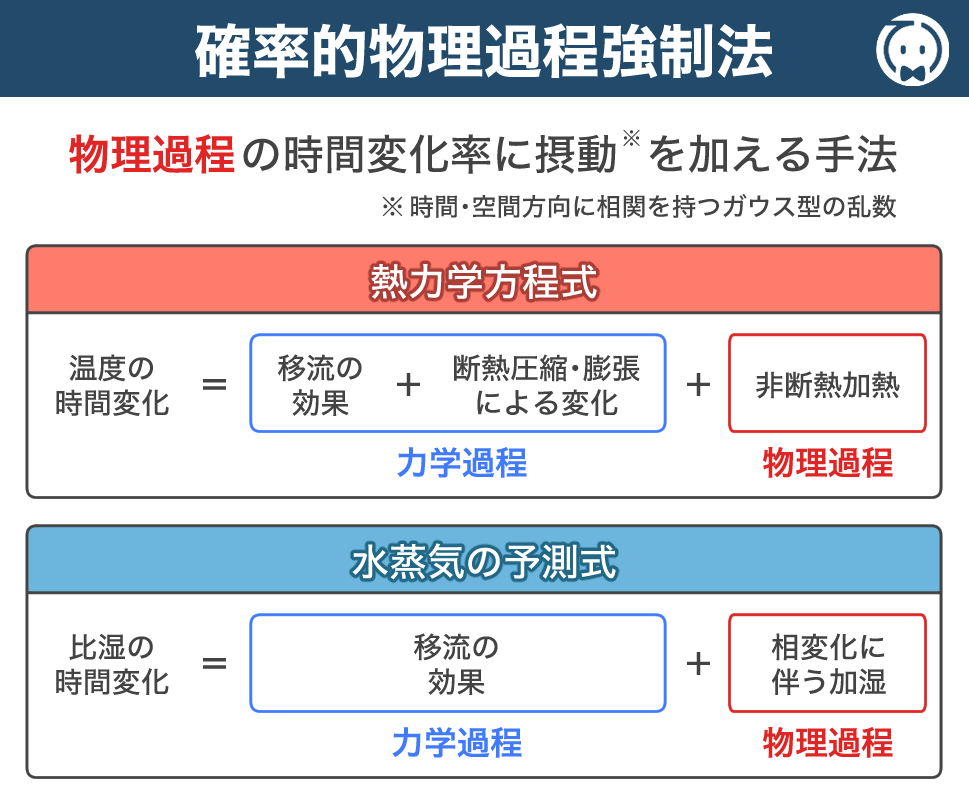
したがって、気象庁のメソアンサンブル予報では、初期値と側面境界値に少しずつ異なった誤差 (摂動) を加えた複数の予測を行っており、確率的物理過程強制法が導入されていますので、答えは 正 となります。

本問の解説：(d) について

（問題）アンサンブル予報を利用する際の留意点として、メンバー間のばらつきが大きい時は、(d)気象要素の日々の変動が大きくなる予測である ことを示している。

→ 答えは 誤 です。

アンサンブル予報では、メンバー間のばらつきが大きい場合、初期値や物理過程に含まれる微小な誤差が時間の経過とともに増幅しやすい大気の状態であることを意味します。

例えば、特定の予報時間においてメンバー間で予測値が大きく異なる場合、その時間の予測に含まれる不確実性が大きく、信頼度が低いと考えられます。

逆に、メンバー間のばらつきが小さい場合、予測の信頼性が高いとみなされます。

したがって、アンサンブル予報を利用する際の留意点として、メンバー間のばらつきが大きい時は、「気象要素の日々の変動が大きくなる予測である」ではなく「予測の不確実性が大きい」ことを示していますので、答えは 誤 となります。

以上より、本問の解答は、(d) のみ誤り とする ４ となります。