問7
図は、軸対称の気圧分布・風速分布をもつ低気圧の中心とその周辺の気温及び気圧の分布を、高度1000mから 2000mの範囲で模式的に示したものである。この低気圧に伴う風と気圧について述べた次の文章の下線部 (a) ~ (d) の正誤の組み合わせとして正しいものを、下記の1~5の中から1つ選べ。ただし、この低気圧の範囲では静力学平衡、及び傾度風平衡が成り立っており、コリオリパラメーターは一定、風向はどの高さでも同じとする。また、以下の文では気圧差は高い気圧から低い気圧を引いた差であり、すべて正である。
傾度風平衡にあるこの低気圧においては (a) 気圧傾度力がコリオリ力と遠心力の和と釣り合っている。また、この低気圧では、どの高度でも中心に近いほど高温であった。このとき、2つの高度1000m、2000mで考えると、静力学平衡の仮定より、中心Oの周辺の点Rにおける2つの高度間の気圧差ΔPRは、中心Oにおける2つの高度間の気圧差ΔPOより (b) 大きい。このことから、高度2000mにおける2点O’、R’間の気圧差ΔP2000は高度1000mの2点O、R間の気圧差ΔP1000より (c) 小さいことが分かる。これらのことから、中心ほど高温で軸対称な分布を持つこの低気圧においては、高度が高くなるほど風速は (d) 小さくなることが分かる。
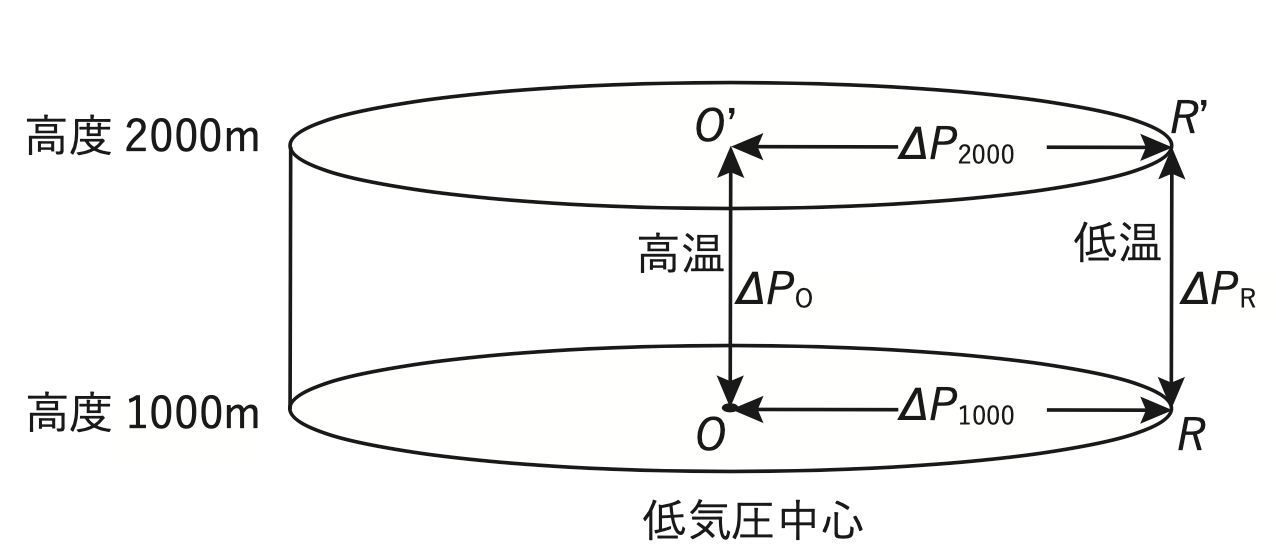
(問題)図は、軸対称の気圧分布・風速分布をもつ低気圧の中心とその周辺の気温及び気圧の分布を、高度1000mから 2000mの範囲で模式的に示したものである。この低気圧に伴う風と気圧について述べた次の文章の下線部 (a) ~ (d) の正誤の組み合わせとして正しいものを、下記の1~5の中から1つ選べ。ただし、この低気圧の範囲では静力学平衡、及び傾度風平衡が成り立っており、コリオリパラメーターは一定、風向はどの高さでも同じとする。また、以下の文では気圧差は高い気圧から低い気圧を引いた差であり、すべて正である。
傾度風平衡にあるこの低気圧においては (a) 気圧傾度力がコリオリ力と遠心力の和と釣り合っている。また、この低気圧では、どの高度でも中心に近いほど高温であった。このとき、2つの高度1000m、2000mで考えると、静力学平衡の仮定より、中心Oの周辺の点Rにおける2つの高度間の気圧差ΔPRは、中心Oにおける2つの高度間の気圧差ΔPOより (b) 大きい。このことから、高度2000mにおける2点O’、R’間の気圧差ΔP2000は高度1000mの2点O、R間の気圧差ΔP1000より (c) 小さいことが分かる。これらのことから、中心ほど高温で軸対称な分布を持つこの低気圧においては、高度が高くなるほど風速は (d) 小さくなることが分かる。

本問は、静力学平衡および傾度風平衡が成り立つ場合における、低気圧中心と周囲との気圧差および風速差に関する問題です。
本問の解説:(a) について
→ 答えは 正 です。
ここでは、傾度風平衡にある低気圧において (a) 気圧傾度力がコリオリ力と遠心力の和と釣り合っているかどうかを考えます。
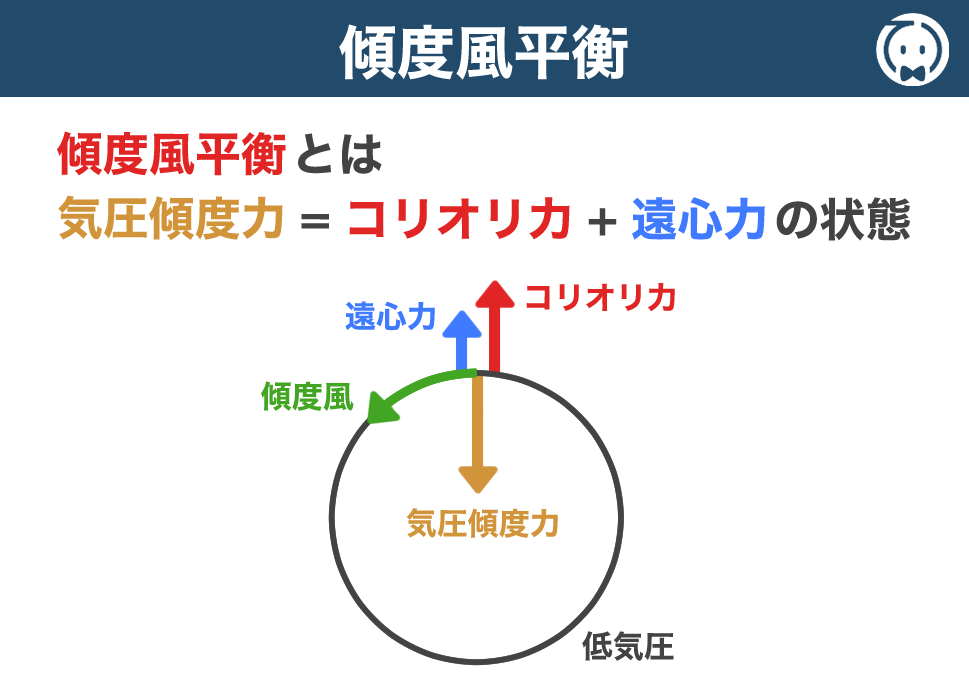
北半球にある低気圧では、
気圧傾度力 は気圧の高い外側から内側に向かって働きます。
コリオリ力 は風向の直角右方向に働きますので、外向きの力になります。
遠心力 はもちろん外向きに働きます。
これら3つの力が釣り合った状態を、傾度風平衡 といいます。
したがって、傾度風平衡にある低気圧において、気圧傾度力はコリオリ力と遠心力の和と釣り合っていますので、答えは 正 となります。
今回は北半球の場合で考えていますが、実は南半球でも下線部 (a) の結果は正しくなります。
なぜなら、南半球ではコリオリ力は北半球とは逆向きに、風向に対して直角左方向に働きますが、低気圧の風向は時計回り(北半球とは逆向き)ですので、コリオリ力は外向きに働くことになるためです。
なお、高気圧の場合、気圧傾度力は外向き、コリオリ力は内向きになり、コリオリ力が気圧傾度力と遠心力の和と釣り合うことになります。
本問の解説:(b) について
(問題)中心Oの周辺の点Rにおける2つの高度間の気圧差ΔPRは、中心Oにおける2つの高度間の気圧差ΔPOより (b) 大きい。
→ 答えは 正 です。
ここでは、ΔPO <ΔPR であるかどうかを考えます。
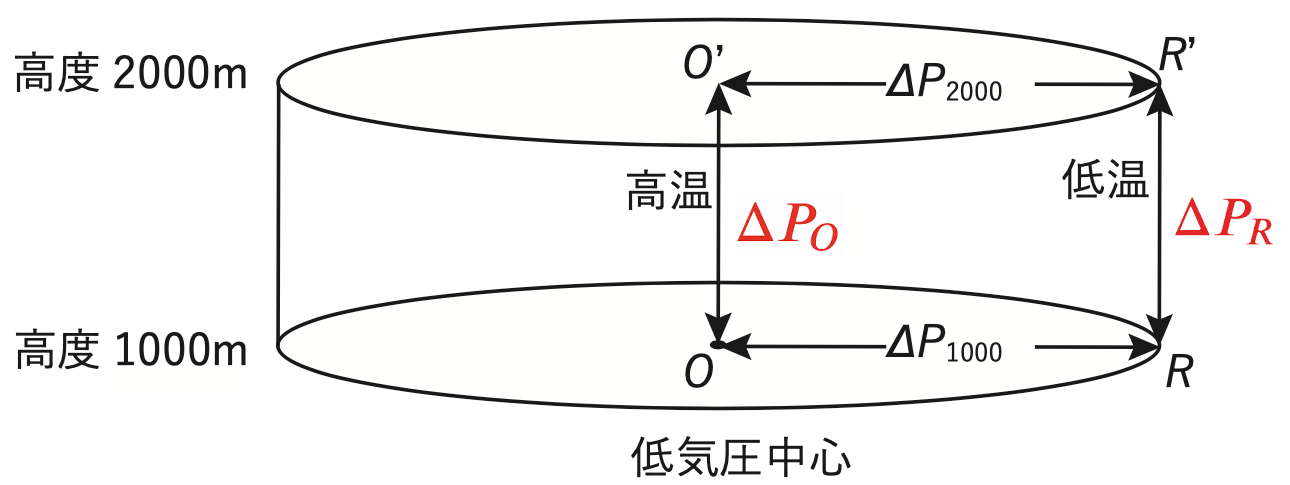
この問題は 静力学平衡 の式から解くことができます。
静力学平衡とは、2つの等圧面の気圧差が、その間に挟まれた空気の単位面積当たりの重さに等しい状態のことをいいます。
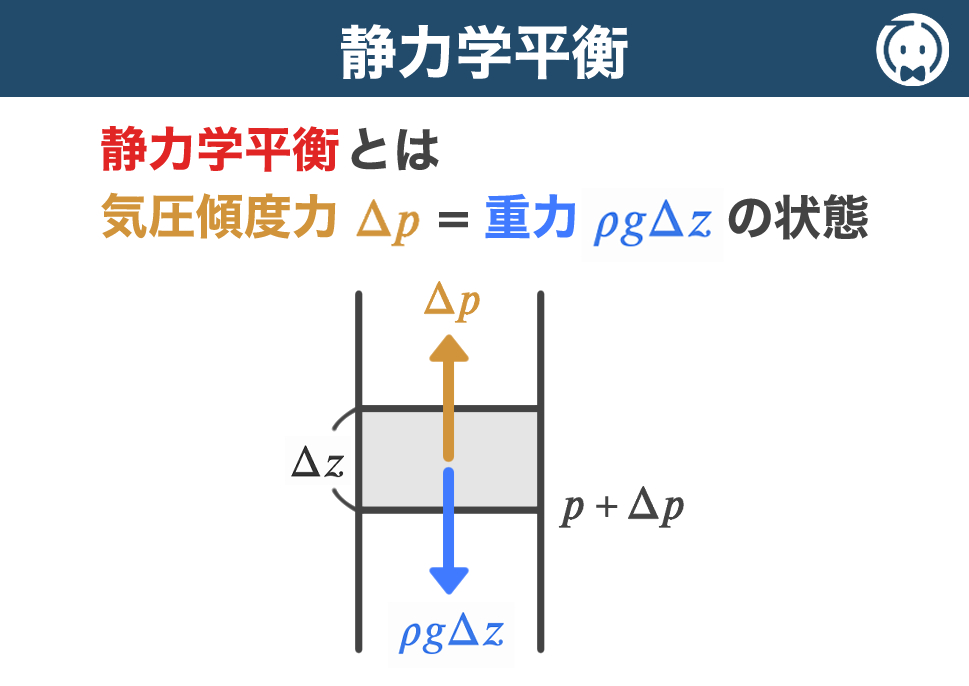
上図において、微小な高度幅 \( \Delta z \) にある空気の単位面積当たりの重さは \( \rho g \Delta z \) ( \( \rho \) は密度、\( g \) は重力の加速度)なので、上下面の気圧差 \( \Delta p \) は、鉛直上向きを正とすると
\( \Delta p = \, – \rho g \Delta z \tag{b-1}\)
\( \Delta p = \, – \rho g \Delta z \tag{b-1}\)
となります。
(b-1)式を使って、ΔPO と ΔPR 間の静力学平衡の式をそれぞれ表すと以下のようになります。
( \(\rho_O\)、\(\rho_R\) はそれぞれ ΔPO、ΔPR 間の密度)
\( \Delta P_O = \, – \rho_O g \Delta Z \tag{b-2}\)
\( \Delta P_O = \, – \rho_O g \Delta Z \tag{b-2}\)
\( \Delta P_R = \, – \rho_R g \Delta Z \tag{b-3}\)
\( \Delta P_R = \, – \rho_R g \Delta Z \tag{b-3}\)
ここで、\(\Delta Z\) は1000m(高度2000m – 高度1000m)で同じですので、
(b-2)式、(b-3)式は以下のように変形することができます。
\( \displaystyle \Delta Z=\ – \frac{\Delta P_O}{\rho_O g} =\ – \frac{\Delta P_R}{\rho_R g} \tag{b-4}\)
\( \displaystyle \Delta Z=\ – \frac{\Delta P_O}{\rho_O g} =\ – \frac{\Delta P_R}{\rho_R g} \tag{b-4}\)
(b-4)式より、マイナスと重力加速度 g を削除して
\( \displaystyle \frac{\Delta P_O}{\rho_O} = \frac{\Delta P_R}{\rho_R}\tag{b-5}\)
\( \displaystyle \frac{\Delta P_O}{\rho_O} = \frac{\Delta P_R}{\rho_R}\tag{b-5}\)
となります。
ここで、問題文の条件「この低気圧では、どの高度でも中心に近いほど高温であった。」より、
\( T_O > T_R \) となることが分かります。
気温が高いと言うことは、空気が膨張して密度が小さくなるため、
\( \rho_O < \rho_R \) と考えることもできます。
したがって、 (b-5)式において、\( \rho_O < \rho_R \) が成り立ちますので、等式を成り立たせるためには ΔPO <ΔPR でなければなりません。
以上より、中心Oの周辺の点Rにおける2つの高度間の気圧差ΔPR は、中心Oにおける2つの高度間の気圧差ΔPO より大きい(=ΔPR >ΔPO) ので答えは 正 となります。
本問の解説:(c) について
→ 答えは 正 です。
ここでは、高度2000mにおける2点O’、R’間の気圧差ΔP2000 が、高度1000mの2点O、R間の気圧差ΔP1000 より (c) 小さい かどうかを考えます。
つまり、ΔP2000 <ΔP1000 であるかどうかを考えます。
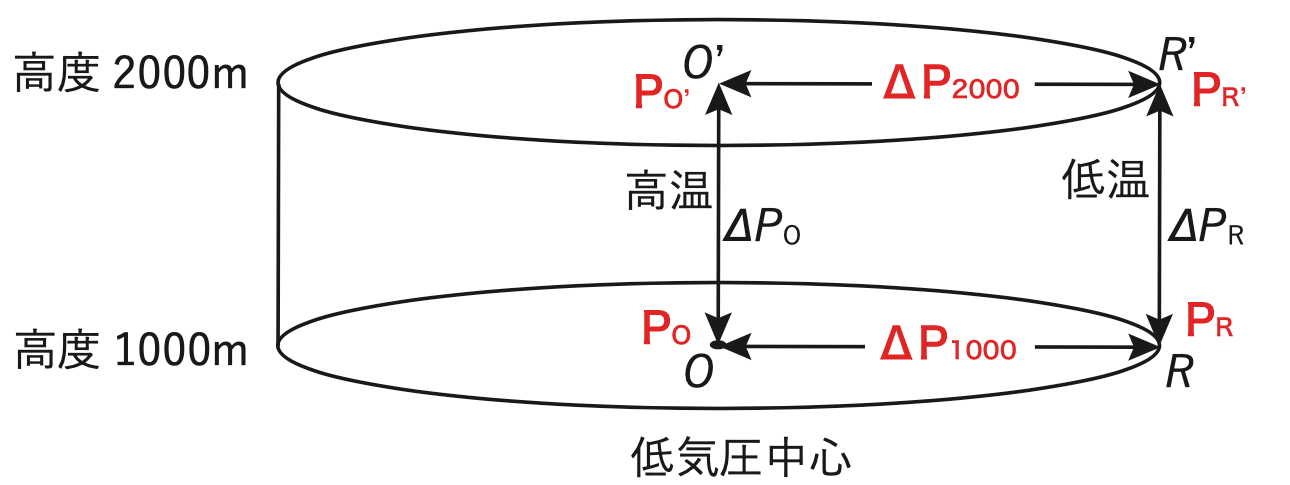
中心O、O’、点R、R’の気圧をそれぞれ PO 、PO’ 、PR 、PR’ として考えます。
下線部(b)の結果から、点Rは中心Oに比べて鉛直方向の気圧減少量が大きいので
(c-1)
ΔPO <ΔPR
(c-1)
ΔPO <ΔPR
となります。
また、ΔPO とΔPR は高度1000mと高度2000mの気圧差ですので、ΔPO>0、ΔPR>0とすると
(c-2)
ΔPO = PO – PO’
(c-3)
ΔPR = PR – PR’
(c-2)
ΔPO = PO – PO’
(c-3)
ΔPR = PR – PR’
と書けます。
(c-1)式に(c-2)式、(c-3)式をそれぞれ代入すると
(c-4)
PO – PO’ < PR – PR’
(c-4)
PO – PO’ < PR – PR’
となります。
さらに、低気圧は中心の方が気圧が低いので、PO < PR であり、ΔP1000 とΔP2000 はそれぞれ中心OとR、O’とR’の気圧差ですので、ΔP1000>0、ΔP2000>0とすると
ΔP1000 = PR – PO
ΔP1000 = PR – PO
↓移項して
(c-5)
PO = PR – ΔP1000
(c-5)
PO = PR – ΔP1000
ΔP2000 = PR’ – PO’
ΔP2000 = PR’ – PO’
↓移項して
(c-6)
PO’ = PR’ – ΔP2000
(c-6)
PO’ = PR’ – ΔP2000
と書けます。
(c-4)式に(c-5)式、(c-6)式をそれぞれ代入すると
(PR – ΔP1000) – (PR’ – ΔP2000) < PR – PR’
(PR – ΔP1000) – (PR’ – ΔP2000) < PR – PR’
↓括弧を外して
PR – ΔP1000 – PR’ + ΔP2000 < PR – PR’
PR – ΔP1000 – PR’ + ΔP2000 < PR – PR’
↓PR と PR’ を削除して
ΔP2000 < ΔP1000
ΔP2000 < ΔP1000
以上より、ΔP2000 < ΔP1000 (=高度2000mにおける2点O’、R’間の気圧差ΔP2000 は高度1000mにおける2点O、R間の気圧差ΔP1000 より小さい)となりますので、答えは 正 となります。
本問の解説:(d) について
→ 答えは 正 です。
ここでは、この低気圧において、高度が高くなるほど風速は (d) 小さくなるかどうかを考えます。
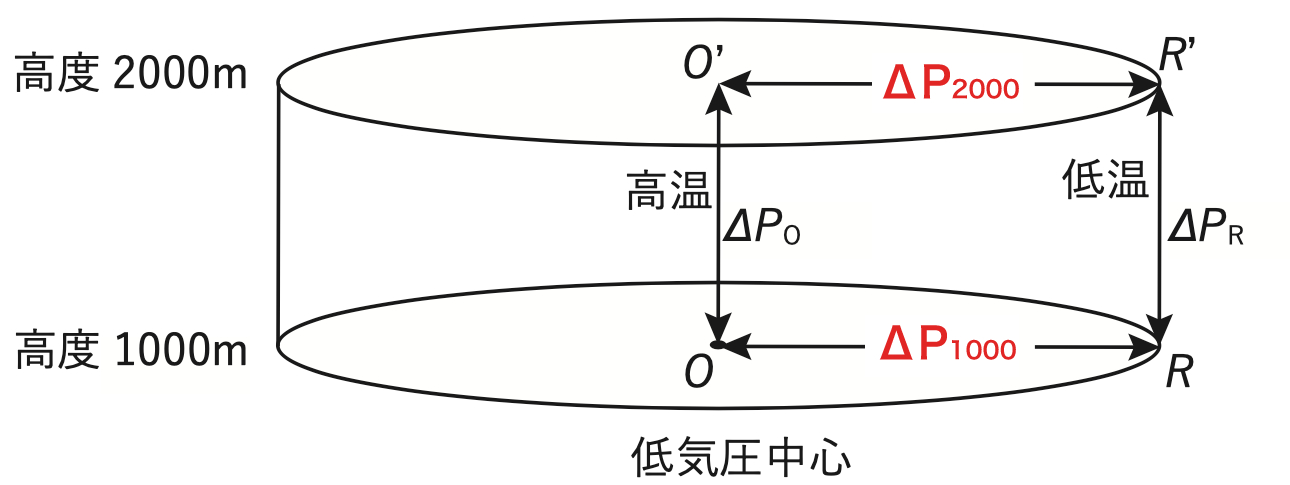
風は気圧が高い方から低い方に向かって吹き、気圧傾度が大きいほど、風速は大きくなります。
下線部(c)の結果から、高度2000mにおける2点O’、R’間の気圧差ΔP2000 は高度1000mにおける2点O、R間の気圧差ΔP1000 より小さいので
ΔP2000 < ΔP1000
ΔP2000 < ΔP1000
となります。
つまり、高度が高くなるほど気圧傾度は小さくなり、風速も小さくなるので、答えは 正 となります。
以上より、本問の解答は、(a) 正 (b) 正 (c) 正 (d) 正 とする 1 となります。
書いてある場所:P43〜45(静力学平衡)
書いてある場所:P127〜128(静力学平衡)、P131(層厚の式)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。





コメント
コメント一覧 (2件)
O から O’ の平均気圧と R から R’ の平均気圧をともに同じ P という値にしていいものなんでしょうか…?
仮定してるのは静力学平衡なので、
・O と O’ の密度が同じ(ρ とする)、
・R と R’ の密度が同じ(ρ’ とする)、
外より内の方が高温なので ρ < ρ' である、
というこれぐらいのことしか言えない気がします。
cs様
コメントありがとうございます。
ご指摘のとおり、O から O’ の平均気圧と R から R’ の平均気圧をともに同じ P という値にするのは、物理学的に問題があったように思います。
本問(b)は、静力学平衡の式のみで解くことができますので、静力学平衡の式を用いた解法に修正いたしました。
この度は、誤解を招く表現で混乱させてしまい申し訳ございません。
また、ご不明な点がございましたらコメントいただけますと幸いです。
よろしくお願いいたします。