問2
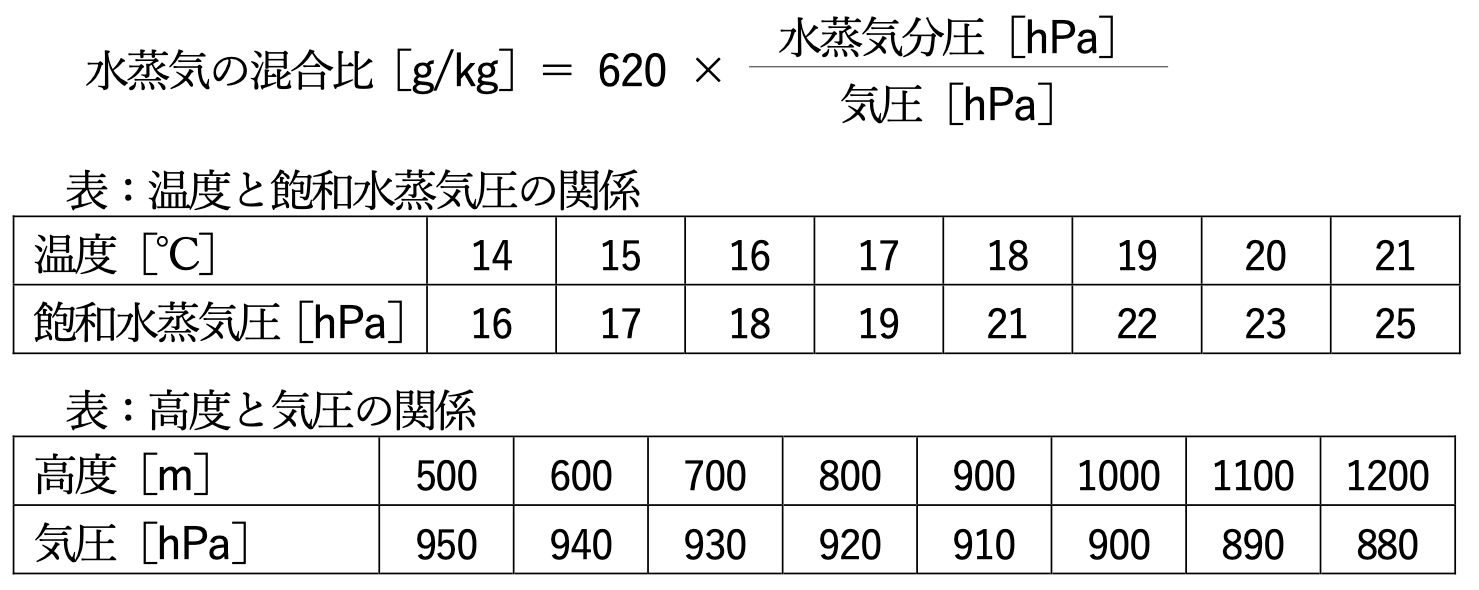
気圧が1000hPa、温度26°C、水蒸気の混合比12.4g/kgの地表近くの空気の持ち上げ凝結高度と、その高度まで持ち上げたときの空気塊の飽和水蒸気圧の組み合わせとして適切なものを、下記の1~5の中から1つ選べ。ただし、乾燥断熱減率は10°C/kmとし、温度と飽和水蒸気圧の関係、及び高度と気圧の関係は以下の表で与えられている。また、水蒸気の混合比は次の式で近似できるとする。
混合比(予備知識)
混合比(読:こんごうひ)とは湿潤空気に含まれる「水蒸気の質量」と「乾燥空気の質量」の比のことです。
 てるるん
てるるん簡単に言うと、水蒸気を含んでいる湿った空気の中で、乾燥空気と水蒸気が何:何の割合で存在しているかを表したものだよ!
簡単な式で書くとこうなります。
\(\text{混合比}=\displaystyle\frac{\text{水蒸気質量 [g]}}{\text{乾燥空気質量 [㎏]}}\)
この式から、本問で与えられている混合比の式を求めてみます。
質量の比は密度の比で考えることもできるので、水蒸気の密度 \( \rho_\nu \) と乾燥空気の密度 \( \rho_d \) を使うと、次のように書くこともできます。
\begin{align} \text{混合比} &= \displaystyle\frac{\rho_\nu}{\rho_d} \end{align}
また、温度 \( T \) の空気塊に含まれる乾燥空気の分圧 \( p_d \) と水蒸気の分圧 \( p_\nu \) は、気体の状態方程式から次のように書くことができます。(\( R_d \)と\( R_\nu \)はそれぞれ乾燥空気と水蒸気の気体定数)
\begin{align} p_d = \rho_d R_d T \\ p_\nu = \rho_\nu R_\nu T \end{align}
また、空気塊の気圧\( p \)は、乾燥空気の分圧 \( p_d \) と水蒸気の分圧 \( p_\nu \)の和で書くことができ、これは周囲の気圧と等しくなります。
\begin{align} p = p_d + p_\nu \end{align}
これらの式と、\( p \gg p_\nu \)であることを用いると、混合比を次のように近似することができます。
\begin{align} \text{混合比} &= \displaystyle{\frac{R_d}{R_\nu}\frac{p_\nu}{p_d}} \\ &= \displaystyle{\frac{R_d}{R_\nu}\frac{p_\nu}{p – p_\nu}} \\ &\sim \displaystyle{\frac{R_d}{R_\nu}\frac{p_\nu}{p}}\end{align}
気体定数の比は分子量の比の逆数に等しいことと、乾燥空気と水の分子量がそれぞれ29と18であることを用いれば、次のように書くことができます。
\begin{align} \text{混合比} &\sim \displaystyle{\frac{18}{29}\frac{p_\nu}{p_d}} \\ &= 0.62 \displaystyle{\frac{p_\nu}{p_d}}\end{align}
最後に混合比の単位をg/kgにするために、右辺を1000倍すれば、本問の式
\begin{align} \text{水蒸気の混合比[g/kg]} &= 620 × \displaystyle{\frac{p_\nu}{p_d}} \\ &= 620 × \displaystyle{\frac{\text{水蒸気分圧 [hPa]}}{\text{気圧 [hPa]}}} \end{align}
\begin{align} \text{水蒸気の混合比[g/kg]} &= 620 × \displaystyle{\frac{p_\nu}{p_d}} \\ &= 620 × \displaystyle{\frac{\text{水蒸気分圧 [hPa]}}{\text{気圧 [hPa]}}} \end{align}
を導くことができました。
また、混合比は乾燥空気と水蒸気の重さの比ですので、空気塊が飽和しなければ、どれだけ上昇、下降しても一定です。
本問の解説
(問題)気圧が1000hPa、温度26°C、水蒸気の混合比12.4g/kgの地表近くの空気の持ち上げ凝結高度と、その高度まで持ち上げたときの空気塊の飽和水蒸気圧の組み合わせとして適切なものを、下記の①~⑤の中から1つ選べ。ただし、乾燥断熱減率は10°C/kmとし、温度と飽和水蒸気圧の関係、及び高度と気圧の関係は以下の表で与えられている。また、水蒸気の混合比は次の式で近似できるとする。


①:持ち上げ凝結高度 800m 飽和水蒸気圧 21hPa
②:持ち上げ凝結高度 800m 飽和水蒸気圧 20hPa
③:持ち上げ凝結高度 1000m 飽和水蒸気圧 20hPa
④:持ち上げ凝結高度 1000m 飽和水蒸気圧 18hPa
⑤:持ち上げ凝結高度 1000m 飽和水蒸気圧 16hPa
→ 答えは ④:持ち上げ凝結高度:1000m、飽和水蒸気圧:18hPa です。
本問では、地表近くにある空気塊の持ち上げ凝結高度と、持ち上げ凝結高度まで持ち上げた時の飽和水蒸気圧を求めます。
混合比は飽和しなければ、空気塊をどれだけ上昇・下降させても一定です。
つまり、地表近くの空気塊の混合比12.4g/kgは、持ち上げ凝結高度まで持ち上げたとしても12.4g/kgのままであるということです。
(持ち上げ凝結高度は、空気塊が飽和するときの高度ですので、それ以上持ち上げると、混合比は一定ではなくなります。言い換えると、持ち上げ凝結高度は、空気塊の混合比が一定となる上限の高度であり、下層雲の雲底高度とも言えます。)
ですので、空気塊を持ち上げ凝結高度まで持ち上げた時の混合比が、問題文で与えられている混合比12.4g/kgと一致するかを求めていけばOKです。
具体的には、選択肢の数字を使って計算していきます。
本問の計算の流れは下記のとおりです。
(1) 持ち上げ凝結高度での空気塊の気温を求める。
(2) (1)で求めた気温での飽和水蒸気圧を求める。
(3) 水蒸気の混合比を求め、12.4g/kgと一致するか確認する。
選択肢①
(1) 持ち上げ凝結高度での空気塊の気温を求める。
持ち上げ凝結高度が800mなので、乾燥断熱減率 (10°C/km) を使うと高度800mでの空気塊の気温は
26℃ – (10℃/km × 800m) = 18℃
となります。
(2) (1)で求めた気温での飽和水蒸気圧を求める。
表 (温度と飽和水蒸気圧の関係) より、18℃の空気塊の飽和水蒸気圧は21hPaとなります。
選択肢の飽和水蒸気圧も21hPaとなっているので、ここまで矛盾はなさそうです。
(3) 水蒸気の混合比を求め、12.4g/kgと一致するか確認する。
表 (高度と気圧の関係) より、高度800mでの気圧は920hPaです。
(2) より水蒸気分圧 (飽和水蒸気圧) は21hPaです。
問題で与えられた式を使うと
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{21}{920} \\ &= 14.2 \end{align}
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{21}{920} \\ &= 14.2 \end{align}
となり、空気塊の混合比 12.4 [g/kg] と一致しないので、選択肢①は 誤 となります。
選択肢②
選択肢②では、持ち上げ凝結高度が800mのとき、飽和水蒸気圧は20hPaとなっています。
選択肢①で求めたように、高度800mでの空気塊の気温18℃に対応する飽和水蒸気圧は21hPaなので、この時点で計算せずとも、選択肢②は 誤 となります。
選択肢③
(1) 持ち上げ凝結高度での空気塊の気温を求める。
持ち上げ凝結高度が1000mなので、高度1000mでの空気塊の気温は
26℃ – (10℃/km × 1000m) = 16℃
となります。
(2) (1)で求めた気温での飽和水蒸気圧を求める。
表 (温度と飽和水蒸気圧の関係) より、16℃の空気塊の飽和水蒸気圧は18hPaとなります。
しかし、選択肢では、飽和水蒸気圧は20hPaとなっているので、この時点で選択肢②は 誤 となります。
選択肢④
持ち上げ凝結高度については、選択肢③と同じなので、(2) から考えてみましょう。
(2) (1)で求めた気温での飽和水蒸気圧を求める。
表 (温度と飽和水蒸気圧の関係) より、16℃の空気塊の飽和水蒸気圧は18hPaとなります。
選択肢の飽和水蒸気圧も18hPaとなっているので、ここまで矛盾はなさそうです。
(3) 水蒸気の混合比を求め、12.4g/kgと一致するか確認する。
表 (高度と気圧の関係) より、高度1000mでの気圧は900hPaです。
(2) より水蒸気分圧 (飽和水蒸気圧) は18hPaです。
問題で与えられた式を使うと
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{18}{900} \\ &= 12.4 \end{align}
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{18}{900} \\ &= 12.4 \end{align}
となり、空気塊の混合比 12.4 [g/kg] と一致するので、選択肢④が 正 となります。
選択肢⑤
すでに答えは分かりましたが、確認のため選択肢⑤についても考えておきましょう。
(1) 持ち上げ凝結高度での空気塊の気温を求める。
持ち上げ凝結高度が1200mなので、高度1200mでの空気塊の気温は
26℃ – (10℃/km × 1200m) = 14℃
となります。
(2) (1)で求めた気温での飽和水蒸気圧を求める。
表 (温度と飽和水蒸気圧の関係) より、14℃の空気塊の飽和水蒸気圧は16hPaとなります。
選択肢の飽和水蒸気圧も16hPaとなっているので、ここまで矛盾はなさそうです。
(3) 水蒸気の混合比を求め、12.4g/kgと一致するか確認する。
表 (高度と気圧の関係) より、高度1200mでの気圧は880hPaです。
(2) より水蒸気分圧 (飽和水蒸気圧) は16hPaです。
問題で与えられた式を使うと
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{16}{880} \\ &= 11.3 \end{align}
\begin{align} 水蒸気の混合比 [g/kg] &= 620 × \frac{水蒸気分圧 [hPa]}{気圧 [hPa]} \\ &= 620 × \frac{16}{880} \\ &= 11.3 \end{align}
となり、空気塊の混合比 12.4 [g/kg] と一致しないので、選択肢⑤は 誤 となります。
したがって、答えは ④ となります。
書いてある場所:P61(混合比)
書いてある場所:P48〜49(混合比)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。



コメント