問14
気象の予報の利用者A、B、Cが次の文に示す要望を持っている。関係する気象要素について、気象会社XとYの予報精度の検証結果が下表のとおりであるとき、それぞれの利用者が契約する気象会社として最も適切な選択を、下記の1~5の中から1つ選べ。
利用者A:気温が30℃を超えると、かき氷の需要が増えるので、翌日の最高気温の予報精度が高い方の気象会社と契約したい。
利用者 B:冬の関東平野部で野外イベントを複数回開催する予定である。雨が降ると延期しなければならないので、降水の有無の予報精度が高い方の気象会社と契約したい。
利用者C:降水確率で翌日の商品の入荷数を決めるので、降水確率予報の精度が高い方の気象会社と契約したい。

本問は、利用者のニーズに適合する最適な気象会社を選択する問題です。
問題を解く前に、用語の整理をしておきましょう。
平均誤差
平均誤差(ME:Mean Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の系統的な偏りを評価する指標です。
平均誤差は下式で定義され、予報値から実況値を差し引いた予報誤差の合計を、予報回数で割って求めます。
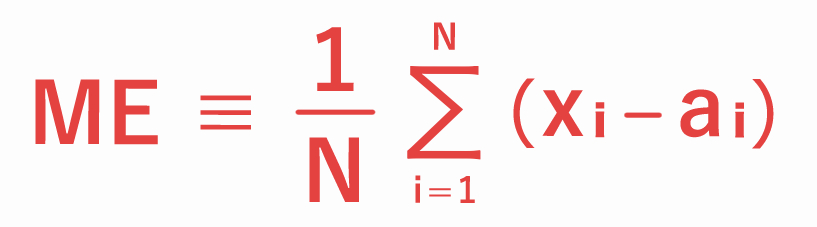
(N:標本の数、xi:予報値、ai:実況値)
平均誤差は、値がプラスであれば予報が過大、マイナスであれば予報が過小であることを意味します。
つまり、値が0のときは、平均的に見て、予報が正にも負にも偏っていないということです。
しかし、正の誤差と負の誤差が打ち消し合う場合にも、値は小さくなりますので、値が小さいほど予報精度が良いわけではありません。
 てるらん
てるらん平均誤差は、実況値に比べて、予報値が全体的に大きいのか、小さいのかを判別する指標なんだね!
二乗平均平方根誤差
二乗平均平方根誤差(RMSE:Root Mean Square Error)とは、量的予報(例:気温、風速など)の誤差(=予報値−実況値)の大きさを評価する指標です。
二乗平均平方根誤差は下式で定義され、予報値と実況値の誤差を二乗して平均し、その平方根を取って求めます。
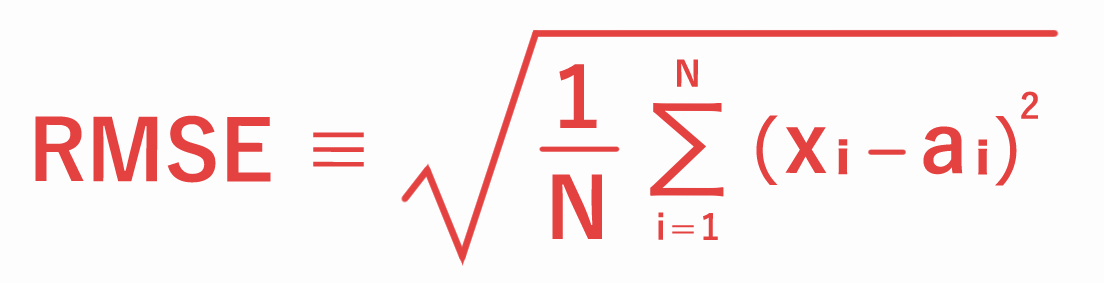
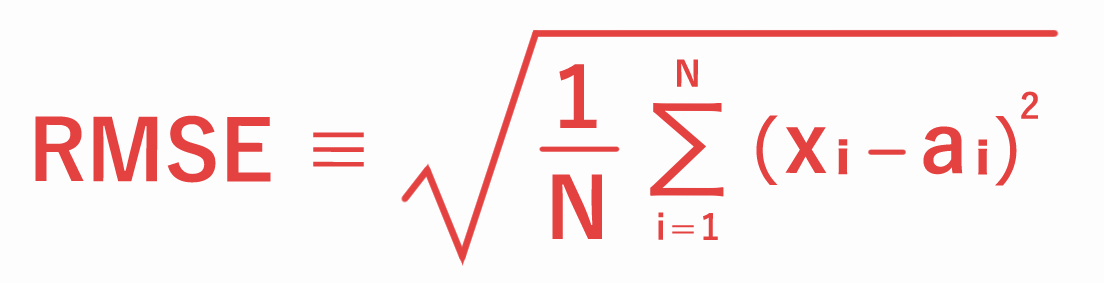
(N:標本の数、xi:予報値、ai:実況値)
二乗平均平方根誤差は、誤差を二乗していますので、誤差の正負(系統的な偏り)ではなく、誤差の大きさを評価します。
つまり、値が0に近いほど予報精度が良く、値が大きいほど誤差が大きいということです。



平均誤差は、予報誤差の偏りを評価していたのに対して、
二乗平均平方根誤差は、予報誤差の大きさを評価しているんだよ!
スレットスコア
スレットスコア(TS:Threat Score) とは、現象の発生頻度が少なく、発生を予想することの意味が大きい現象(例:太平洋側の降水、雷など)の予報精度を評価する指標です。
スレットスコアは下式で定義され、発生頻度が少ない現象をどれくらい正しく予報できたかを評価するために、事例数が多い「予報なし・実況なし」を除いた適中率で求めます。
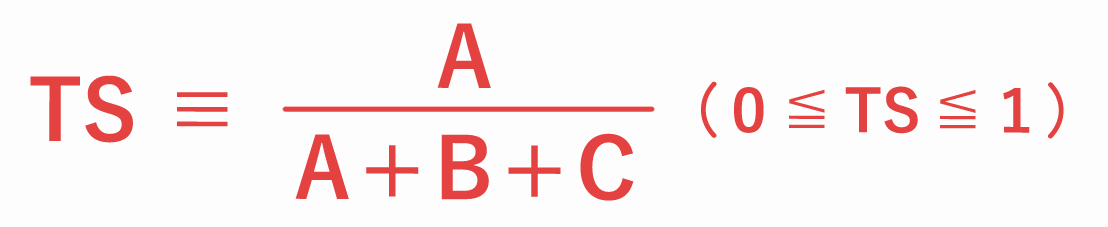
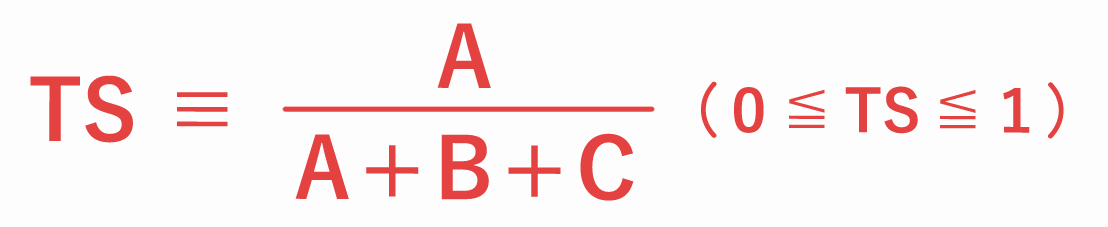
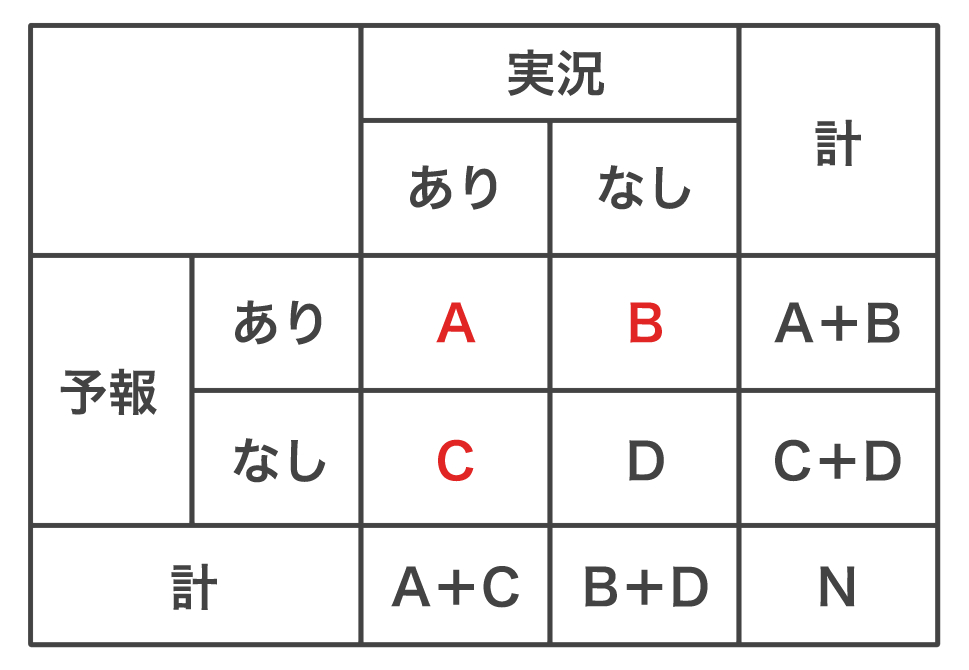

スレットスコアは0〜1までの値をとり、1に近いほど予報精度が良く、0に近いほど予報精度が悪い、と評価されます。



スレットスコアは、あまり発生しない現象をどれくらい予報できていたかを判別する指標なんだね!
ブライアスコア
ブライアスコア(BS:Brier Score) とは、確率で予測する予報(例:降水確率)と実際の結果の誤差を評価する指標です。
ブライアスコアは下式で定義され、確率予報値と実況値の差の二乗を平均して求めます。


(N:標本数、pi:確率予報値(0〜1(例:予報確率80%=0.8))、
ai:実況値(現象ありで1、現象なしで0))
ブライアスコアは0〜1までの値をとり、0に近いほど予報精度が良く、1に近いほど予報精度が悪い、と評価されます。



ブライアスコアは、降水確率のような、確率予報の精度を評価する指標だよ!
本問の解説:利用者Aについて
(問題)気温が30℃を超えると、かき氷の需要が増えるので、翌日の最高気温の予報精度が高い方の気象会社と契約したい。


→ 答えは Y です。
翌日の最高気温という、量的予報の精度を検証するためには、二乗平均平方根誤差を使用します。
二乗平均平方根誤差は、0以上の値をとり、0に近いほど精度が良いと評価されます。
問題の表を見てみると、Y社の方が二乗平均平方根誤差が小さいので、Y社の方が翌日の最高気温の予報精度が良いことがわかります。
ちなみに、平均誤差は、予報の系統的な偏りを示す指標です。
平均誤差は、X社とY社で符号の違いはあるものの、平均的にみると偏りは同じであり、予報精度が高いかどうかは判断できません。
したがって、翌日の最高気温の予報精度が高いのはY社ですので、答えは Y となります。
本問の解説:利用者Bについて
(問題)冬の関東平野部で野外イベントを複数回開催する予定である。雨が降ると延期しなければならないので、降水の有無の予報精度が高い方の気象会社と契約したい。


→ 答えは Y です。
降水の有無の予報精度という、現象の有無の精度を検証するためには、スレットスコアを使用します。
スレットスコアは、0〜1までの値をとり、1に近いほど精度が良いと評価されます。
問題の表を見てみると、Y社の方がスレットスコアが大きいので、Y社の方が降水の有無の予報精度が良いことが分かります。
したがって、降水の有無の予報精度が高いのはY社ですので、答えは Y となります。
本問の解説:(c)について
(問題)降水確率で翌日の商品の入荷数を決めるので、降水確率予報の精度が高い方の気象会社と契約したい。


→ 答えは Y です。
降水確率予報という、確率予報の精度を検証するためには、ブライアスコアを使用します。
ブライアスコアは、0〜1までの値をとり、0に近いほど精度が良いと評価されます。
問題の表を見てみると、Y社の方がブライアスコアが小さいので、Y社の方が降水確率予報の予報精度が良いことが分かります。
したがって、降水確率予報の精度が高いのはY社ですので、答えは Y となります。
以上より、本問の解答は、(利用者A) Y (利用者B) Y (利用者C) Y とする 5 となります。
書いてある場所:ー
書いてある場所:ー
書いてある場所:P304〜320(予報精度評価)
書いてある場所:P452〜463(予報精度の評価)
書いてある場所:P186〜192(予報精度評価の種類)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。








コメント