問5
雲の中の水滴の併合過程による成長について述べた次の文章の空欄 (a) 〜 (c) に入る数式と語句の組み合わせとして正しいものを、下記の1~5の中から1つ選べ。ただし、水滴はすべて球体であり、小さな水滴の落下速度は0 (ゼロ) とする。
図のように、質量 m の小さな水滴が単位体積当たりの数密度 n で一様に分布している雲の中を、小さな水滴よりも十分に大きい半径 R の水滴が鉛直下向きに速さ W で落下している。大きな水滴が、通過する空間内のすべての小さな水滴を併合するとしたとき、大きな水滴の質量の単位時間あたりの増加量は (a) である。質量の増加に伴い、大きな水滴の半径が表面全体 (表面積 4πR2) で一様に増加するとすれば、単位時間の半径の増加量は (b) に比例する。このとき、W が R1/2 に比例するとすれば、水滴が大きくなるとともに単位時間の半径の増加量は (c) なる。
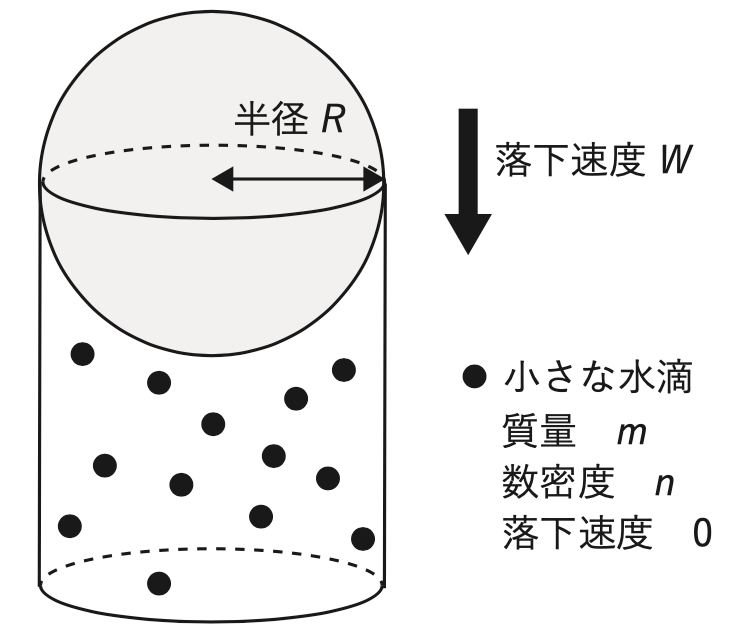
本問は、雲中の水滴の併合過程による成長に関する問題です。
本問の解説:(a)について
(問題)図のように、質量 m の小さな水滴が単位体積当たりの数密度 n で一様に分布している雲の中を、小さな水滴よりも十分に大きい半径 R の水滴が鉛直下向きに速さ W で落下している。大きな水滴が、通過する空間内のすべての小さな水滴を併合するとしたとき、大きな水滴の質量の単位時間あたりの増加量は (a) である。

→ 答えは πmnR2W です。
大きな水滴が単位時間 ( Δt = 1とする ) あたりに通過する空間の体積 V は、
底面積 ( πR2 [m2] ) × 高さ ( W [m/s] × 1 [s] ) で表すことができるので
V = πR2W
となります(下図参照)。
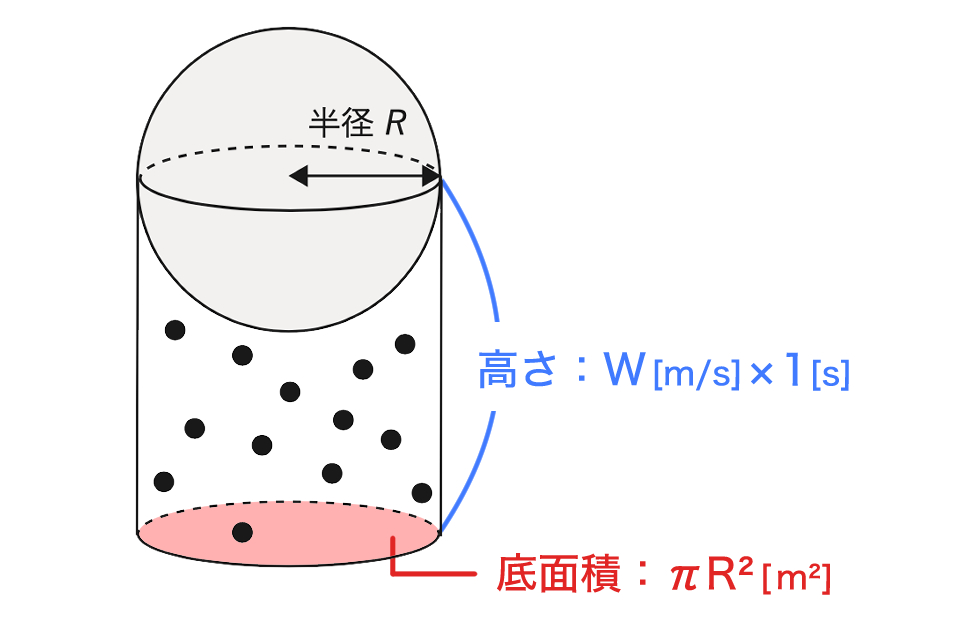
また、体積 V の中にある小さな水滴を全て併合して吸収するとすれば、小さな水滴の質量の総和は
質量 ( m [g] ) × 個数 ( n [ 個/m3 ] × V [m3] ) で表すことができるので、大きな水滴の単位時間あたりの質量増加量 ΔM は、
ΔM = m × ( n × V )
= πmnR2W
となります。
したがって、大きな水滴の質量の単位時間あたりの増加量は πmnR2W ですので、答えは πmnR2W となります。
本問の解説:(b)について
(問題)質量の増加に伴い、大きな水滴の半径が表面全体 ( 表面積 4πR2 ) で一様に増加するとすれば、単位時間の半径の増加量は (b) に比例する。
→ 答えは W です。
問題(a)で求めた質量の増加量 ΔM が、大きな水滴の表面 ( 表面積4πR2 ) に一様に広がるとして考えます。
このとき、大きな水滴の体積の増加量 ΔV は、水滴の密度を ρ とすると、
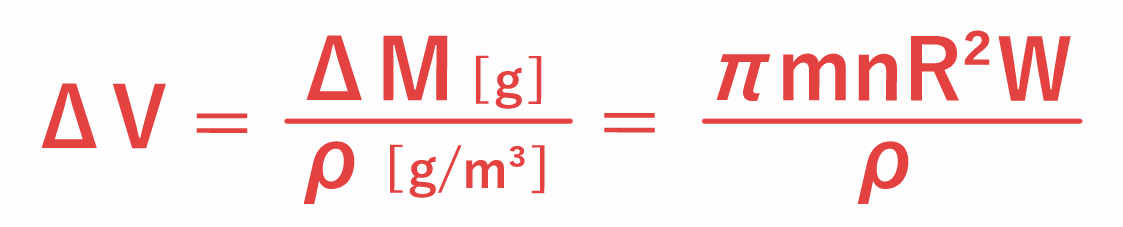
と表すことができます。
また、大きな水滴の体積の増加量 ΔV は、水滴の表面積 4πR2 を底面、水滴の半径の増加量 Δr を高さとする円柱の体積として近似することもできますので、
ΔV = 4πR2Δr
と表すこともできます(下図参照)。
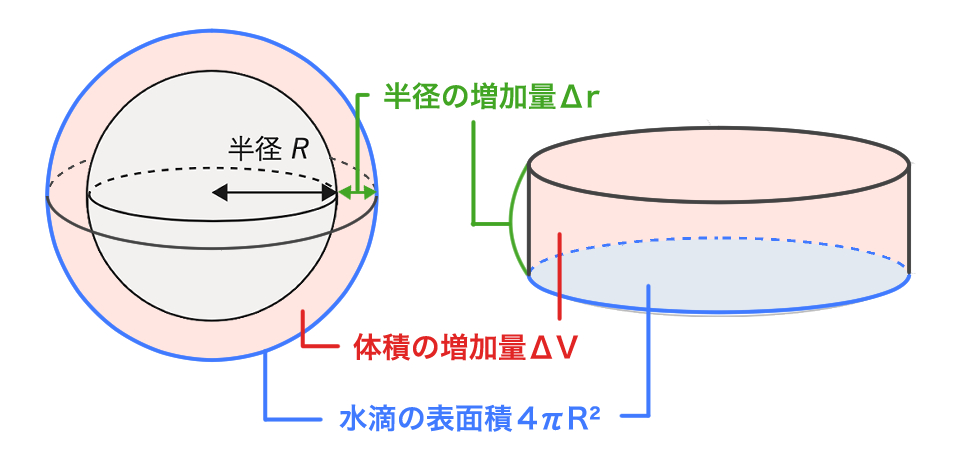
これらが等しいので、
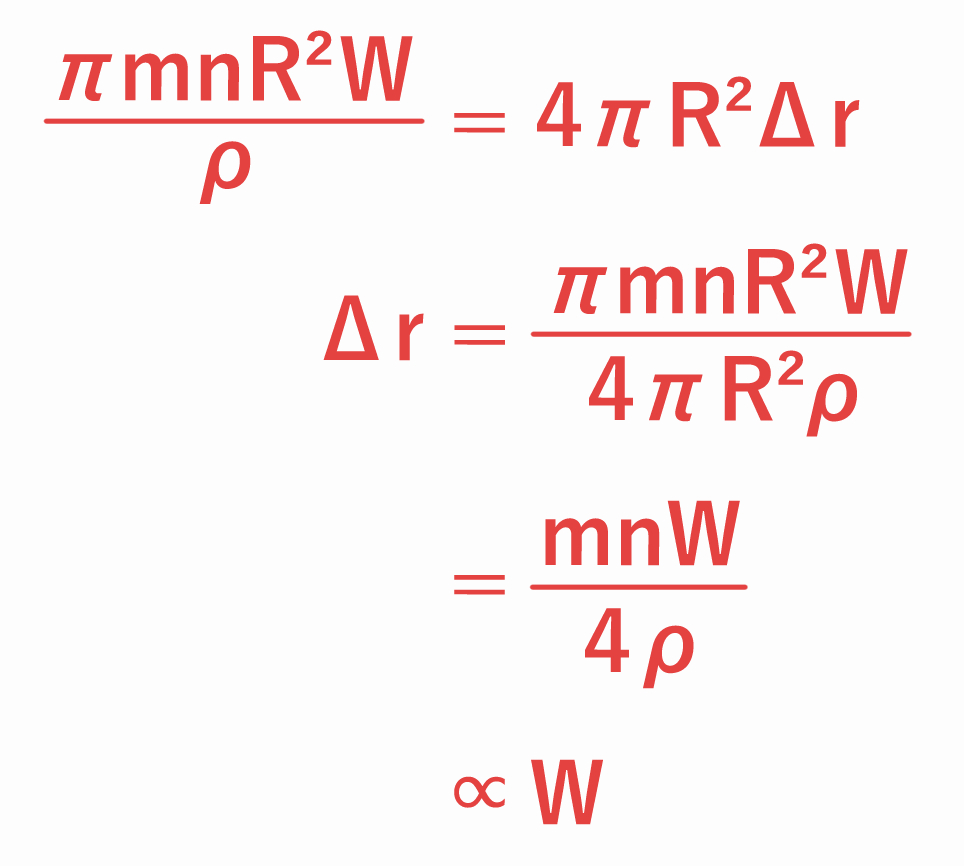
となり、半径の増加量 Δr は、落下速度 W に比例することが分かります。
したがって、質量の増加に伴い、大きな水滴の半径が表面全体 ( 表面積 4πR2 ) で一様に増加するとすれば、単位時間の半径の増加量 Δr は W に比例しますので、答えは W となります。
本問の解説:(c)について
(問題)このとき、W が R1/2 に比例するとすれば、水滴が大きくなるとともに単位時間の半径の増加量は (c) なる。
→ 答えは 大きく です。
問題(b)より、単位時間の半径の増加量 Δr は、落下速度 W に比例します。
また、問題文より W が R1/2 に比例すると仮定しますので、
Δr ∝ W ∝ R1/2
であることが分かります。
したがって、W が R1/2 に比例するとすれば、水滴が大きくなる(= R が大きくなる)とともに単位時間の半径の増加量 Δr は大きくなりますので、答えは 大きく となります。
以上より、本問の解答は、(a) πmnR2W (b) W (c) 大きく とする 4 となります。
書いてある場所:P88〜92(併合過程、雨粒の終端速度)
書いてある場所:P197〜200(併合過程、雨粒の終末速度)
書いてある場所:P145〜149(併合過程、雨粒の終末速度)
書いてある場所:P67〜68(併合過程)、P71〜72(水滴の落下速度)
書いてある場所:P69〜73(併合過程、雨粒の落下速度)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。
本問と同じ分野の問題
記事が見つかりませんでした。








コメント