【第61回】2024年１月試験（学科一般試験）問７（各条件における地衡風の大小関係）

本問は、緯度や気圧傾度から地衡風の大小関係を求める問題です。

地衡風 とは、気圧傾度力とコリオリ力が釣り合って吹く風のことであり、中緯度の上層では水平風に対してこの地衡風の関係が十分に成り立っています。

気圧傾度力 とは、気圧の差（＝気圧傾度）によって生じる力のことです。

下図は水平方向の気圧傾度の模式図です。

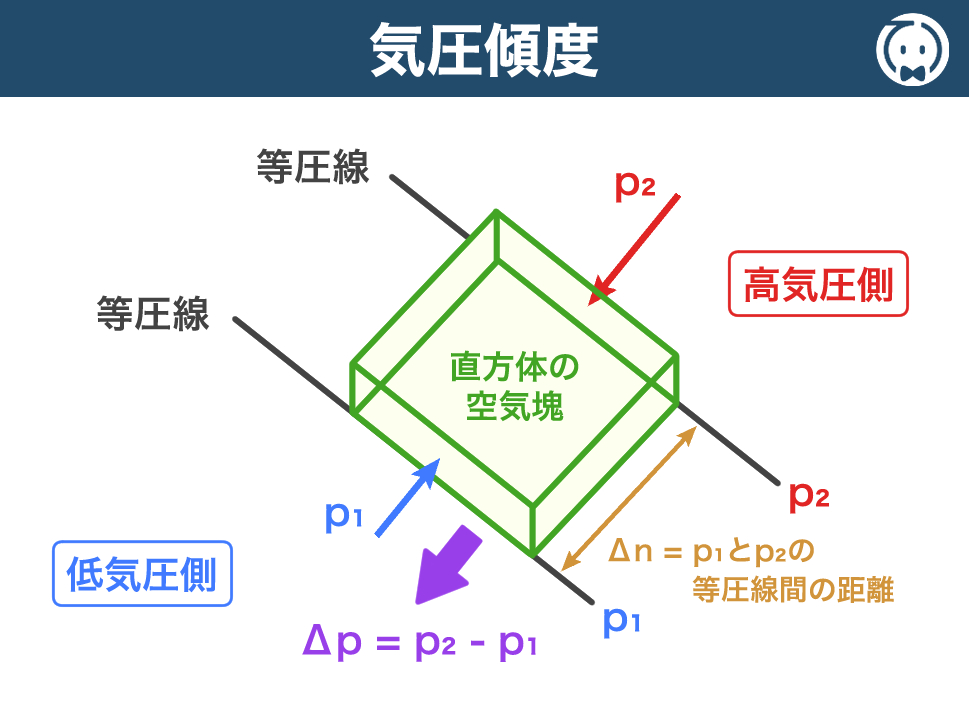
等圧線と等圧線の間にある、直方体の空気塊 を考えます。

このとき、低気圧側の気圧を p₁ 、高気圧側の気圧を p₂ としたとき、その気圧差は Δp＝p₂ – p₁ となります。

これを、p₁ と p₂ の等圧線間の距離 Δn で割ったものを、気圧傾度 といい、

と表されます。

この気圧傾度によって生じる力を 気圧傾度力 といい、高気圧側 → 低気圧側 へと力がはたらきます。

また、空気の密度を ρ とすると、水平方向の気圧傾度力は

と表されます。

コリオリ力 とは、地球の自転によって生じるみかけの力のことです。

単位質量の空気塊に働くコリオリ力は、風速を V 、コリオリパラメータを f とすると、

コリオリ力 = fV　・・・(１)

と表されます。ここで、f（コリオリ・パラメータ）は緯度 φ の関数であり、

f = 2Ωsinφ　・・・(２)

と表されます。（Ω：地球の自転角速度（Ω = 2π/１日 = 7.292 × 10^-5 s^-1））

したがって、(１)式、(２)式より、コリオリ力は

コリオリ力 = 2ΩVsinφ

となります。

地衡風は、気圧傾度力とコリオリ力が釣り合って吹くので、

であり、両辺を2Ωsinφで割ると、地衡風の風速 V は

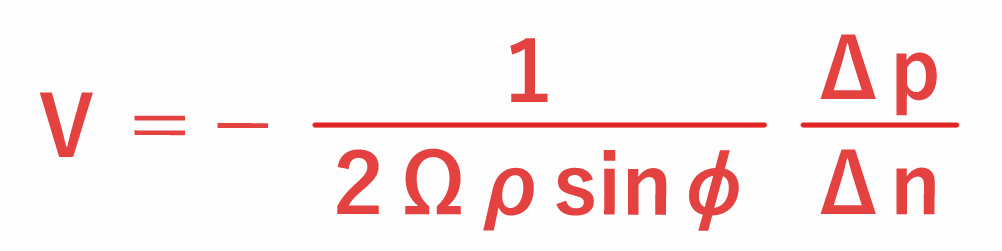
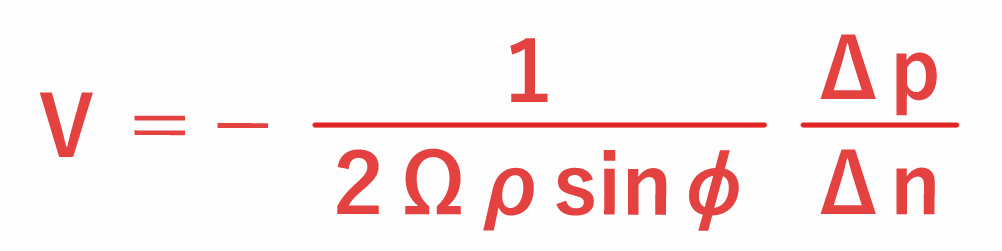
となります。

問題文より、空気の密度 ρ は一定ですので、地衝風の風速 V は、気圧傾度 Δp/Δn に比例し（＝気圧傾度が大きいほど風が強い）、sinφに反比例する（＝低緯度ほど風が強い）ことが分かります。

本問では (a) ～ (d) の条件での地衡風の風速の大小関係を求めれば良いので、分かりやすいように定数部分を K とおくと、地衡風の風速 V は

と書くことができます。（K：-1/2Ωρ(＝比例定数) 、水平気圧傾度：Δp/Δn 、φ：緯度）

以上を踏まえて、(a) ～ (d) の条件での地衡風の風速の大小関係を求めていきましょう。

また、地衡風の風速の大小を比較するだけなので、水平気圧傾度の単位（hPa/100km）は無視し、数値のみ比較すればOKです。

地衡風 (a) の風速

（問題）緯度 30 度（sin30°=0.5）、水平気圧傾度 2 hPa / 100 km

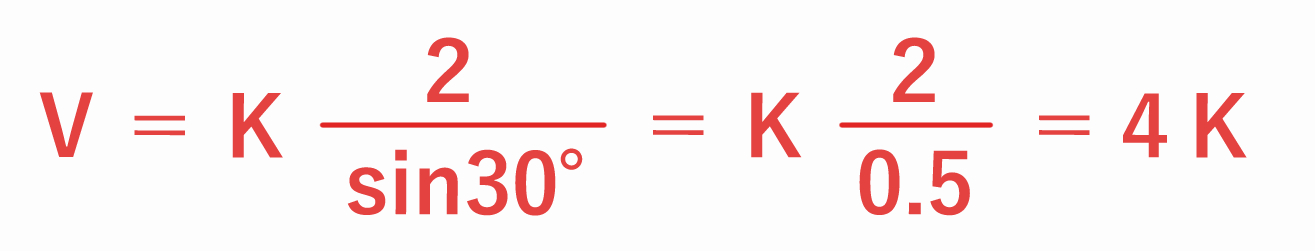
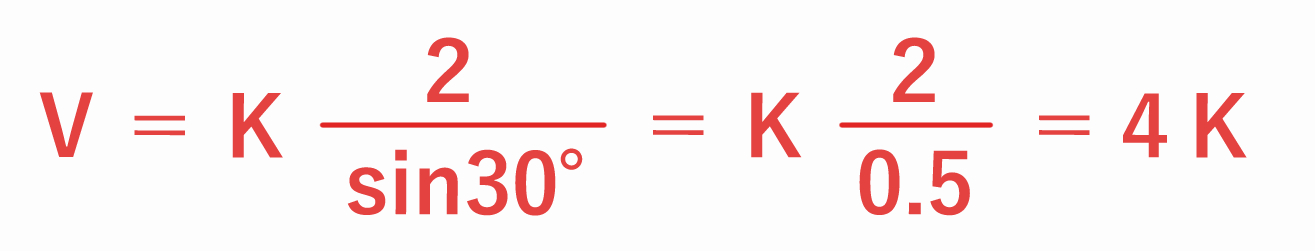
したがって、問題 (a) の地衡風は ４K となります。

地衡風 (b) の風速

（問題）緯度 30 度（sin30°=0.5）、水平気圧傾度 3 hPa / 100 km

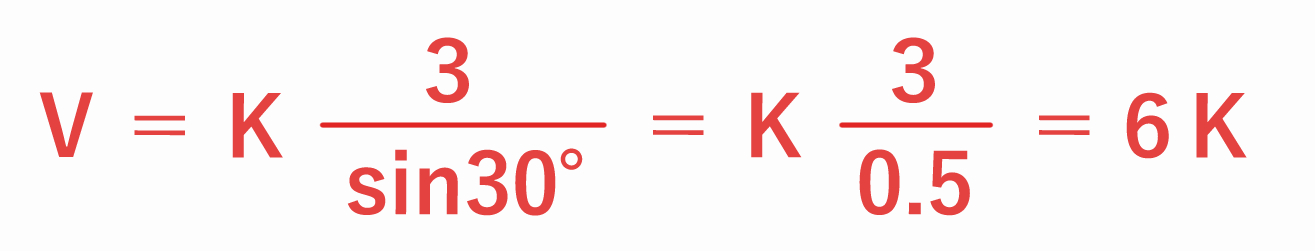
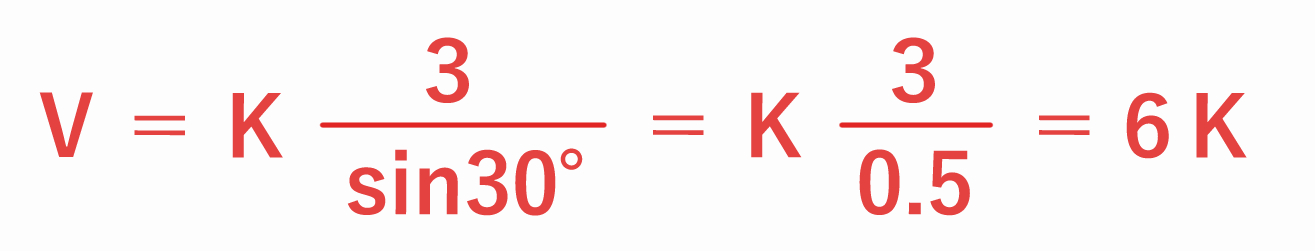
したがって、問題 (b) の地衡風は ６K となります。

地衡風 (c) の風速

（問題）緯度 45 度（sin45°=0.7）、水平気圧傾度 2 hPa / 100 km

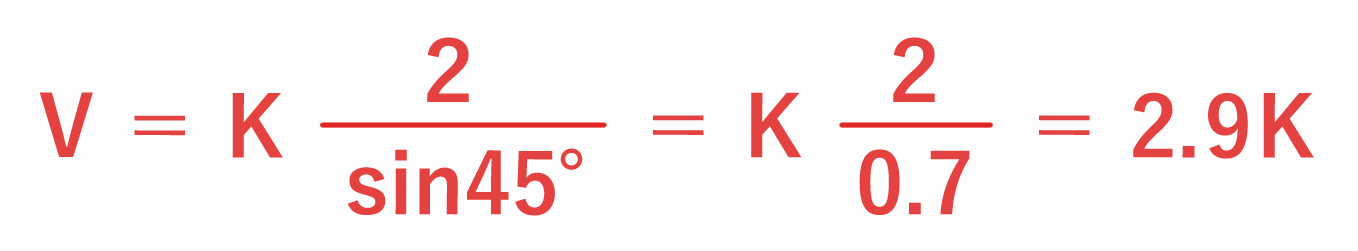
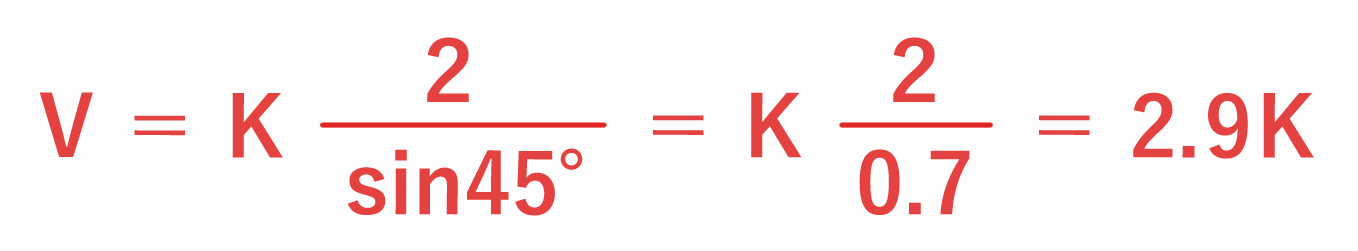
したがって、問題 (c) の地衡風は 2.9K となります。

地衡風 (d) の風速

（問題）緯度 45 度（sin45°=0.7）、水平気圧傾度 3 hPa / 100 km

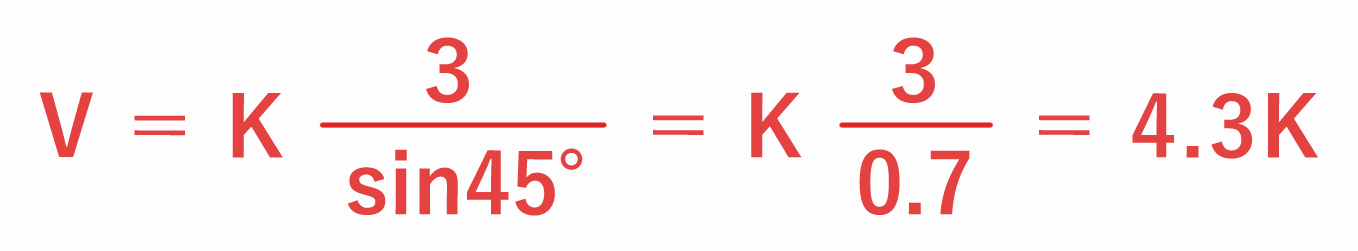
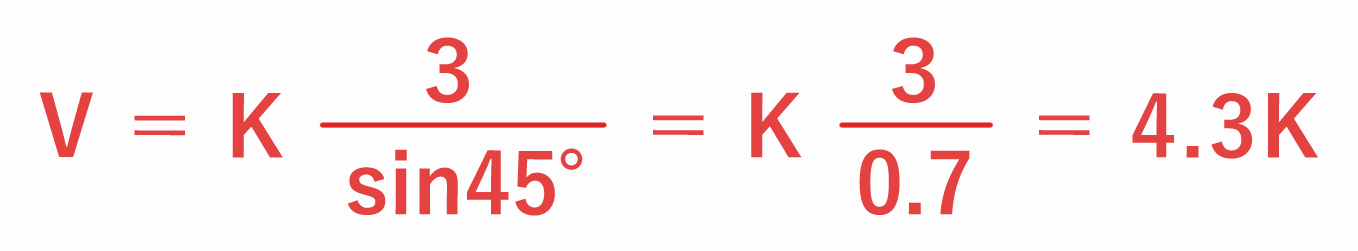
したがって、問題 (d) の地衡風は 4.3K となります。

以上より、本問の解答は、(a) ４K (b) ６K (c) 2.9K (d) 4.3K なので、 (b) ＞ (d) ＞ (a) ＞ (c) とする ２ となります。