問6
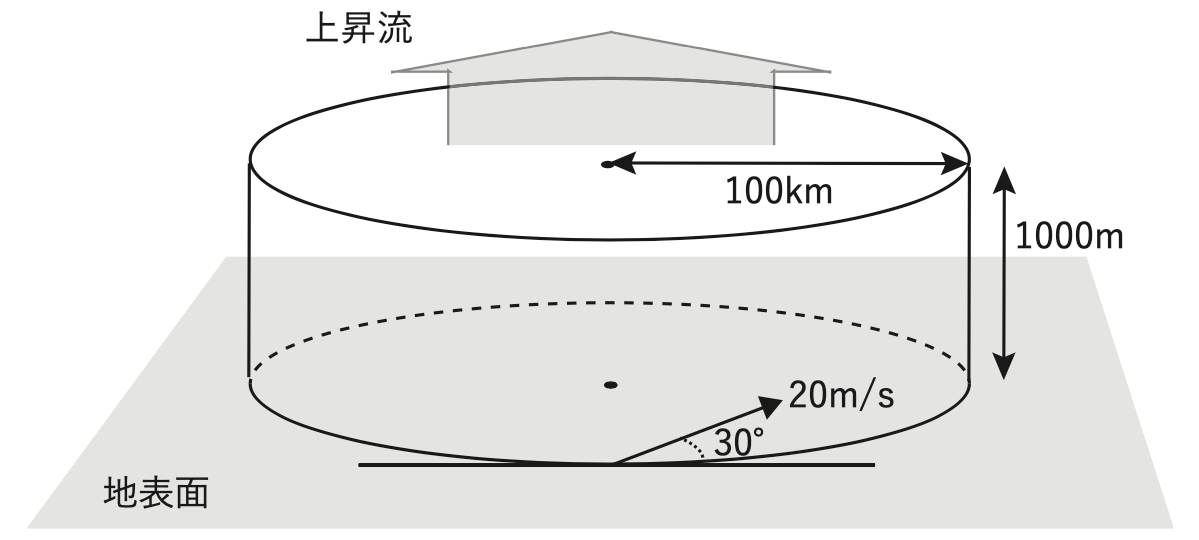
図は、北半球の低気圧の中心付近における空気の収束と上昇流について模式的に示したものである。低気圧中心から半径100kmの円周上のすべての場所で、地表面から高度1000mまで風速20m/sの水平風が接線に対して中心に向かって30°の角度で反時計回りに吹いているとする。高度1000mにおいて、図の円柱の上面で上昇流が一様であるとき、この上昇流の値として適切なものを、下記の1~5の中から1つ選べ。ただし、空気の密度は一定とし、地表面での鉛直流はないものとする。また sin30°=0.5、cos30°=0.9とする。
本問は、質量保存則を用いて、低気圧に収束する空気の流入量から上昇流を求める問題です。
(問題)図は、北半球の低気圧の中心付近における空気の収束と上昇流について模式的に示したものである。低気圧中心から半径100kmの円周上のすべての場所で、地表面から高度1000mまで風速20m/sの水平風が接線に対して中心に向かって30°の角度で反時計回りに吹いているとする。高度1000mにおいて、図の円柱の上面で上昇流が一様であるとき、この上昇流の値として適切なものを、下記の1~5の中から1つ選べ。ただし、空気の密度は一定とし、地表面での鉛直流はないものとする。また sin30°=0.5、cos30°=0.9とする。

→ 答えは 20 cm/s です。
問題の図より、低気圧は半径100km、高さ1000mの円柱形で模式的に表されています。
低気圧への空気の流入は円柱の側面から、低気圧からの空気の流出は円柱の上面から行われており、円柱の底面は地表面なので、流入も流出もありません。
したがって本問は、低気圧への流入量、低気圧からの流出量をそれぞれ求め、質量保存則からこれらが等しいという式を解くことで、上昇流を求めます。
① 低気圧への流入量
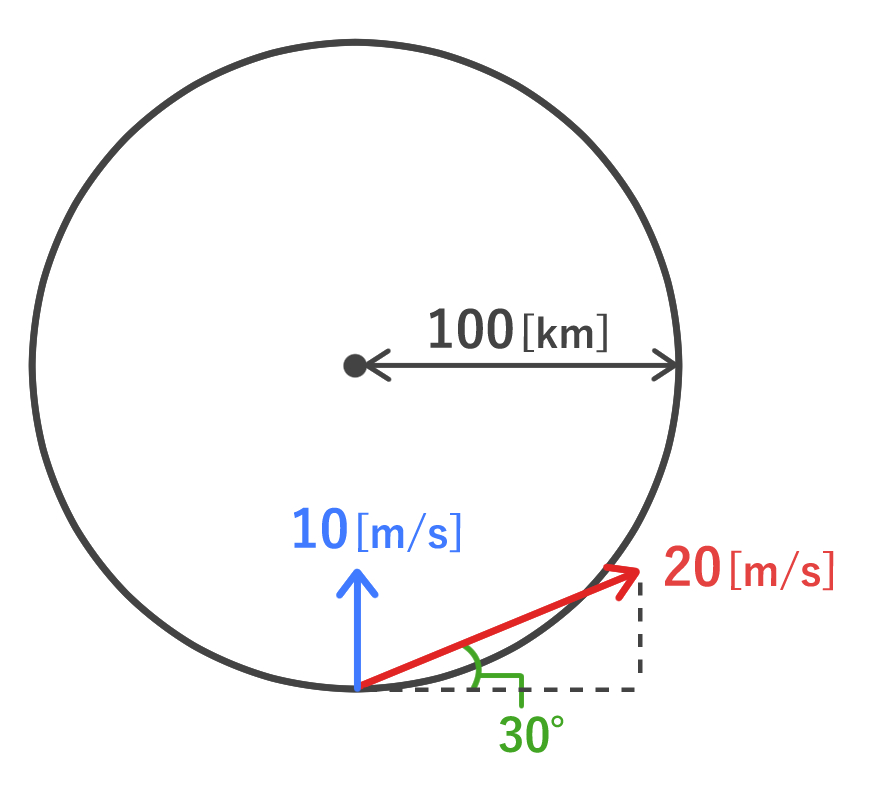
低気圧への流入量は、円柱の側面積に、円の中心に向かう風の成分を掛けた値に等しくなります。
したがって、100 [km] = 105 [m] であることに注意して計算すると

となります。
② 低気圧からの流出量
空気の流出量は、上面の面積を単位時間あたりに通過する空気の体積に等しくなります。
したがって、求める上昇流を W [m/s] とすると、
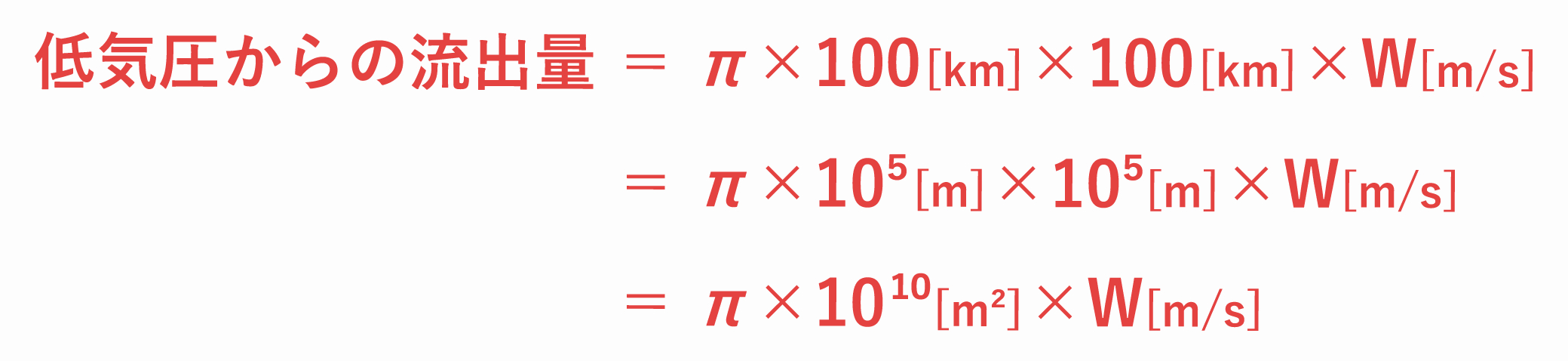
となります。
③ 質量保存則から上昇流を求める
質量保存則より、①で求めた流入量と、②で求めた流出量が等しくなるので
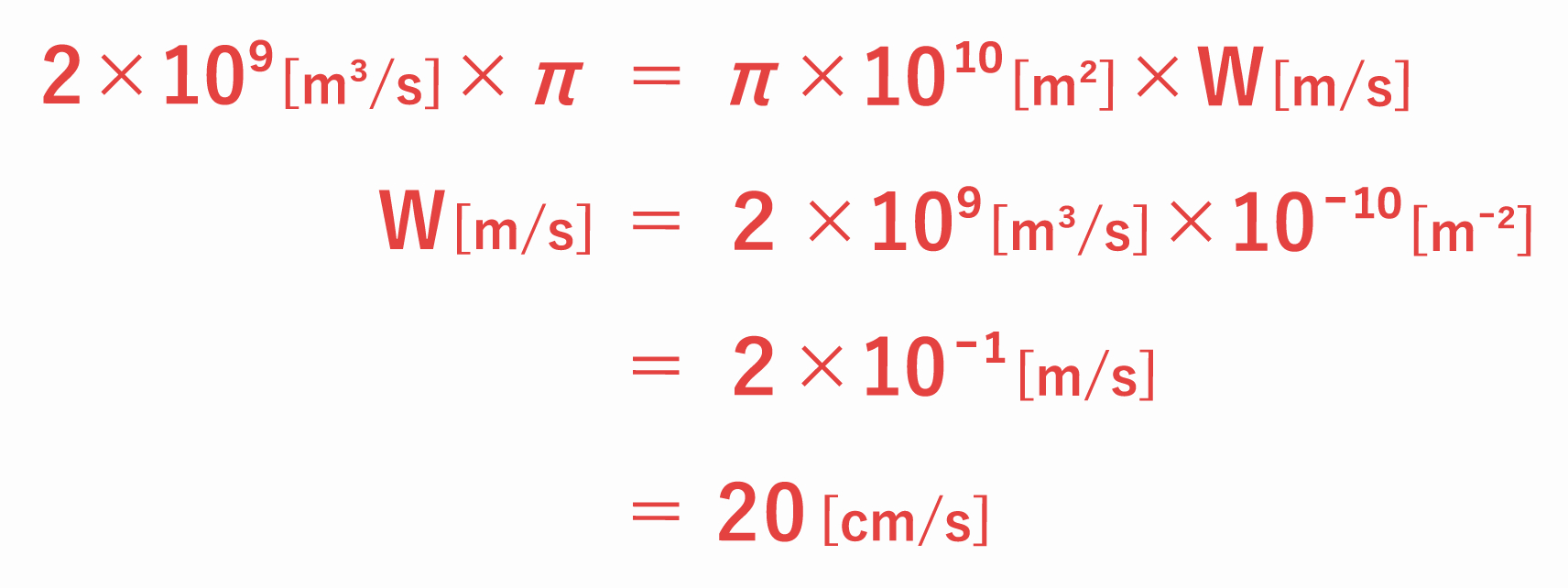
以上より、本問の解答は、20 cm/s とする 3 となります。
書いてある場所:P160〜162(発散・収束)
書いてある場所:P335〜338(発散と収束)
書いてある場所:P266〜267(収束・発散)
書いてある場所:P104〜105(発散と収束)
書いてある場所:P201〜206(発散と収束)
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。






コメント