問6
大気中の点Aにおける気温変化について述べた次の文章の空欄 (a) 、(b) に入る数値の組み合わせとして適切なものを、下記の1~5の中から1つ選べ。ただし、風速と水平方向の気温傾度はどこでも一様とし、sin30°= 0.50、cos30°= 0.87とする。
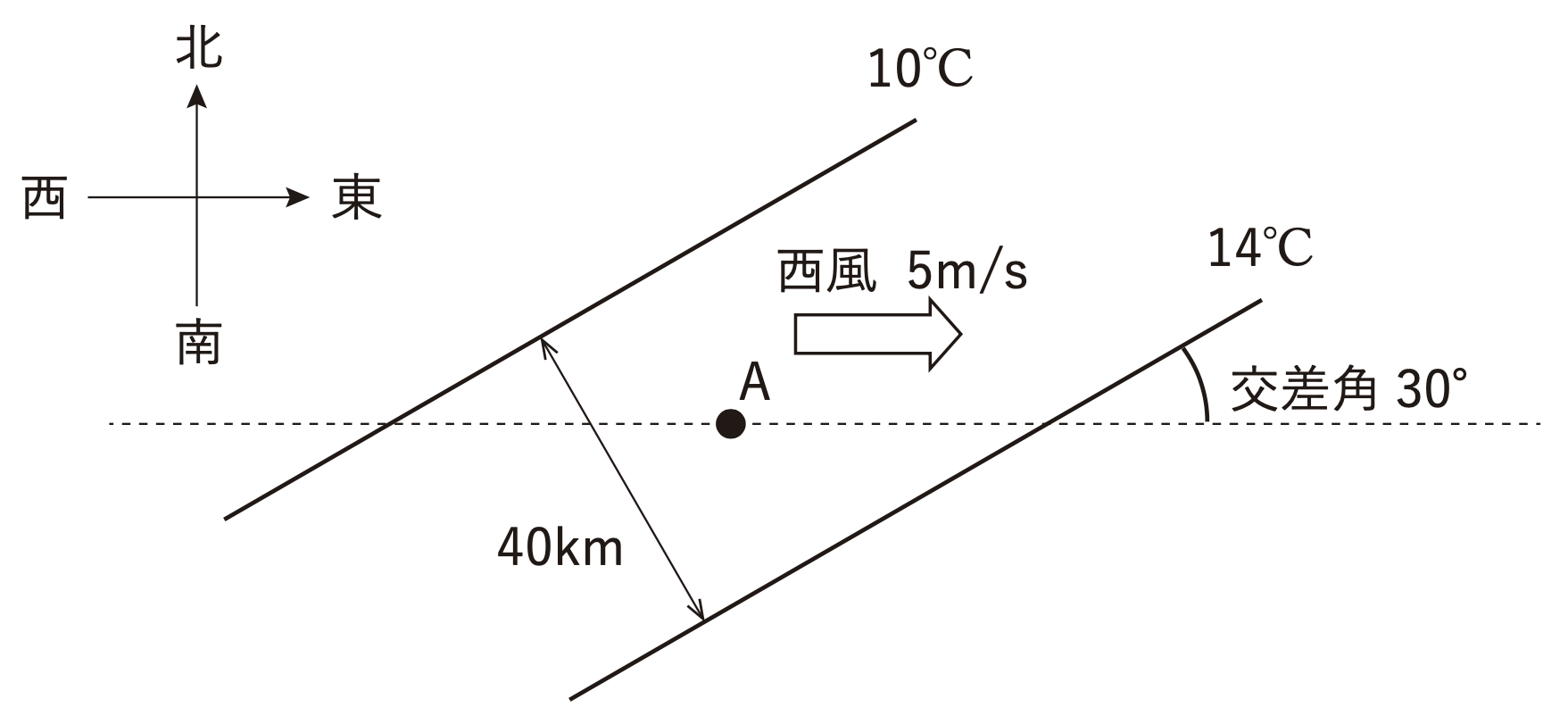
ある高度の水平面上で、図のように10℃と14℃の等温線が40kmの間隔で平行に並び、いずれも東西方向と30°の角度で交差している。また、この水平面上では風速5m/sの西風が吹いている。このとき、2本の等温線の中間にある点Aにおける東西方向の気温傾度は、1kmあたり (a) ℃である。また、点Aにおける移流による気温の時間変化率は、1時間あたり (b) ℃である。
本問は、大気中のある地点の、温度移流による気温変化を求める問題です。
本問の解説:(a) について
(問題)ある高度の水平面上で、図のように10℃と14℃の等温線が40kmの間隔で平行に並び、いずれも東西方向と30°の角度で交差している。また、この水平面上では風速5m/sの西風が吹いている。このとき、2本の等温線の中間にある点Aにおける東西方向の気温傾度は、1kmあたり (a) ℃である。(ただし、風速と水平方向の気温傾度はどこでも一様とし、sin30°= 0.50、cos30°= 0.87とする。)

→ 答えは 0.05 です。
まずは、10℃ と 14℃ の等温線の東西方向の距離を求めましょう。
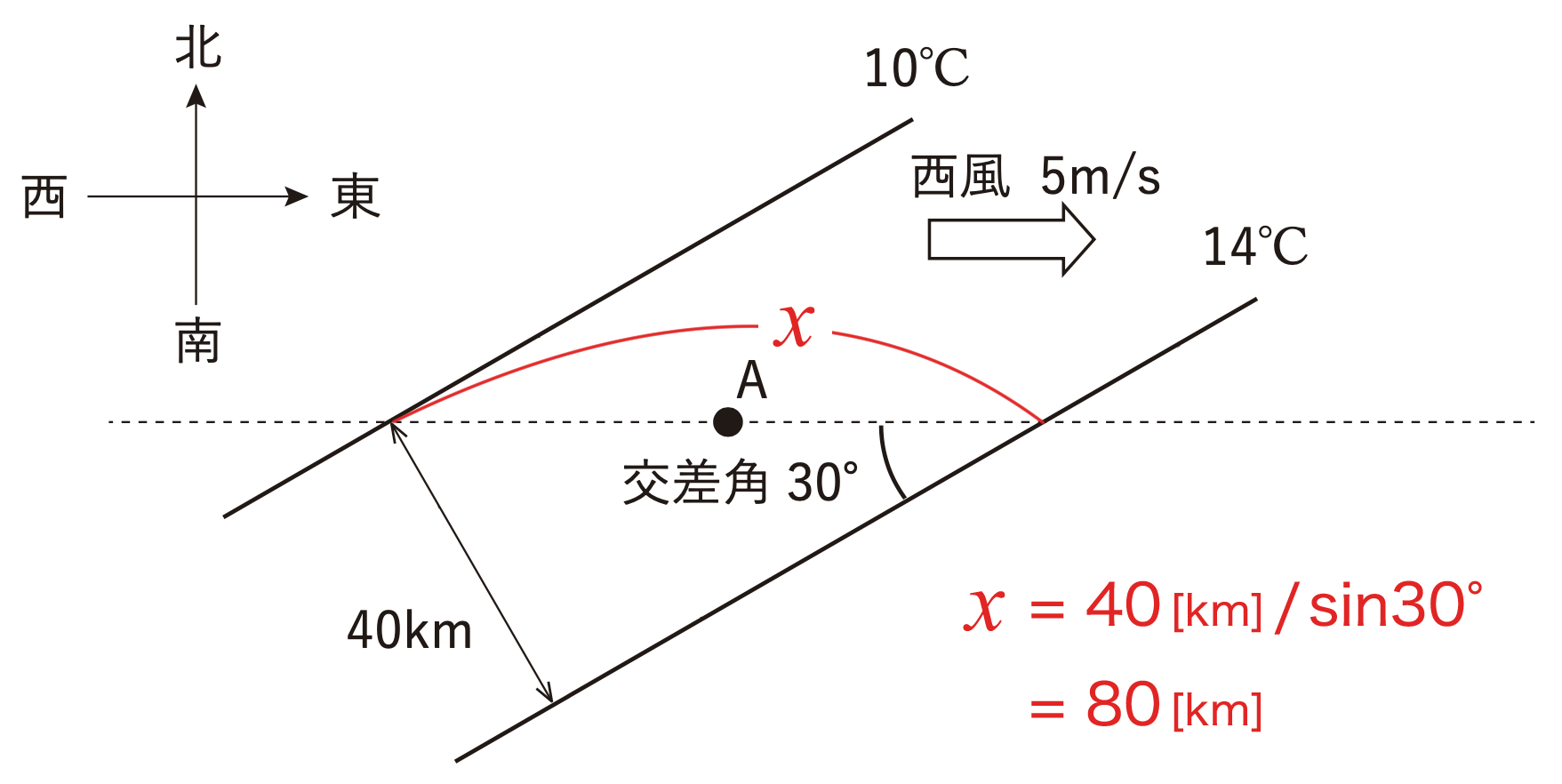
上図のように、三角関数を用いると、10℃ と 14℃ の等温線の東西方向の距離は
40 [km] / sin30°= 80 [km]
となります。
この 80km の間で、気温が4℃ 変化しているので、1kmあたりの東西方向の気温傾度は
4 [℃] / 80 [km] = 0.05 [℃/km]
となりますので、答えは 0.05 となります。
本問の解説:(b) について
(問題)また、点Aにおける移流による気温の時間変化率は、1時間あたり (b) ℃である。

→ 答えは −0.9 です。
ある地点での「移流による」気温の時間変化率 ( 局所時間変化率 ) の評価式は
( ある地点の気温の時間変化率 ) = − ( 風速 ) × ( 風向方向の温度傾度 )
ΔT / Δt = − u × ΔT / Δx
と表すことができます。
(上式は、流体力学のラグランジュ微分 dT/dt = ∂T/∂t + u∂T/∂x において、空気塊の温度が保存される時の dT/dt = 0 より ∂T/∂t + u∂T/∂x = 0 ( つまり局所温度変化が移流だけで決まる ) となるため、局所時間微分 ∂T/∂t を求める式は、ΔT/Δt =− u × ΔT/Δx となります。また一般に、u は東西方向の風速を表し、西風 (東向きの風) を正とします。)
したがって、点Aにおける移流による1時間あたりの気温の時間変化率は、
ΔT / Δt =−5 × 3600 [m/h] × 0.05 / 1000 [℃/m]
= −0.9 [℃/h]
となりますので、答えは −0.9 となります。
(風速は5[m/s] 、東西方向の距離は 0.05 [km] なので、単位を [m] や [h] に揃えるのを忘れないようにしましょう。)
以上より、本問の解答は、(a) 0.05 (b) −0.9 とする 1 となります。
試験問題は「一般財団法人 気象業務支援センター」様の許可を得て掲載しています。
当記事の解説は「一般財団法人 気象業務支援センター」様とは無関係ですので、情報の誤りや不適切な表現があった場合には、お問い合わせからご連絡ください。
また、当記事に掲載された内容によって生じた損害等の一切の責任を負いかねますのでご了承ください。



コメント